Question

【题目】已知函数f（x）=x2+ax+b，实数x1，x2满足x1∈（a-1，a），x2∈（a+1，a+2）．

（Ⅰ）若a＜-，求证：f（x1）＞f（x2）；

（Ⅱ）若f（x1）=f（x2）=0，求b-2a的取值范围．

Answer 1

【答案】（Ⅰ）详见解析（Ⅱ）-＜b-2a＜

【解析】

（Ⅰ）由条件，根据作差法，分解因式，由不等式的性质即可得证；

（Ⅱ）由条件f（x1）=f（x2）=0，x1∈（a-1，a），x2∈（a+1，a+2），结合二次函数的图象可得f（a-1）＞0．f（a）＜0，f（a+1）＜0，f（a+2）＞0，化简整理，结合b，b-2a的范围，即可得到所求范围．

（Ⅰ）证明：因为a＜-，x1＜x2，x1+x2＜2a+2，

所以f（x2）-f（x1）=（x2-x1）（x1+x2+a）＜（x2-x1）（3a+2）＜0，

即f（x1）＞f（x2）；

（Ⅱ）因为f（x1）=f（x2）=0，x1∈（a-1，a），x2∈（a+1，a+2），

所以，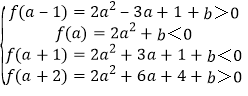

所以max{-2a2+3a-1，-2a2-6a-4}＜b＜min{-2a2，-2a2-3a-1}．

由max{-2a2+3a-1，-2a2-6a-4}＜min{-2a2，-2a2-3a-1}，

解得-＜a＜0．

由于max{-2a2+a-1，-2a2-8a-4}＜b-2a＜min{-2a2-2a，-2a2-5a-1}，

而且max{-2a2+a-1，-2a2-8a-4}≥-，

min{-2a2-2a，-2a2-5a-1}≤，

所以-＜b-2a＜．