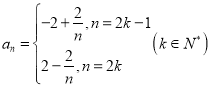题目内容
【题目】在数列
中，若
是正整数，且
，…，则称为“绝对差数列”.
（1）举出一个前5项不为零的“绝对差数列”（只要求写出前10项）；
（2）若“绝对差数列”中，
，数列
满足
，
，…，分别判断当
时，
与
的极限是否存在？如果存在，求出其极限值.
【答案】（1）
，
，
，
，
，
，
，
，
，
．（答案不惟一）
（2）
的极限不存在，
；
【解析】
（1）根据
，
是正整数，且
，
，4，5，
，能够举出一个前五项不为零的“绝对差数列”．
（2）由绝对差数列
中
，
，利用，知该数列自第20项开始．每三个相邻的项周期地取值3，0，3．所以
不存在．．
解：（1），，，，，，，，，．（答案不惟一）
（2）因为在绝对差数列中，．所以自第20项开始，该数列是，，
，
，
，
，
，
，
即自第20项开始．每三个相邻的项周期地取值3，0，3．所以当
时，的极限不存在．
当
时，
，
所以
练习册系列答案
名校课堂系列答案
相关题目
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度，研究人员在某电影院随机抽取了1000名观众作调查，所得结果如下所示，其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
（Ⅰ）完善上述
列联表；
（Ⅱ）是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性？
附：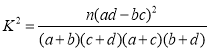
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
