题目内容
如图,在直角三角形ABC中,∠ACB=90°,AB=5,BC=4,AC=3,求三角形ABC绕AB边旋转一周所成几何体的表面积及体积
分析:由已知中直角三角形ABC中,∠ACB=90°,AB=5,BC=4,AC=3,求三角形ABC绕AB边旋转一周所成几何体是两个倒扣的圆锥,其公共的底面是以AB边上的高为半径的圆,两个圆锥的高之和为AB的长,两个圆锥的母线分别是AC,BC的长,求出相关的几何量后,代入圆锥的体积及侧面积公式,即可求出答案.
解答:解:由已知可得三角形ABC绕AB边旋转一周所成几何体为两个底面重合的圆锥
设圆锥的底面半径为R,两圆锥的母线长分别为AC,BC,高之和为AB
则R=2.4
S表面积=πR(AC+BC)=2.4×(3+4)×π=16.8π
V体积=
•πR2•AB=
•(2.4)2•5π=9.6π
设圆锥的底面半径为R,两圆锥的母线长分别为AC,BC,高之和为AB
则R=2.4
S表面积=πR(AC+BC)=2.4×(3+4)×π=16.8π
V体积=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查的知识点是圆锥的侧面积和体积,其中根据旋转体的定义,根据已知求出旋转后圆锥的底面半径,高、母线长等关键的几何量,是解答本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
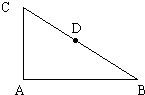 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,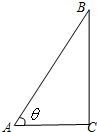 如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S
如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S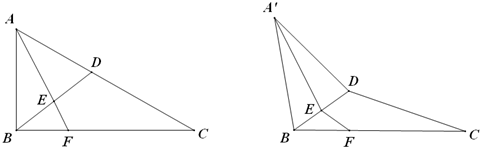
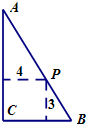 (2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )
(2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )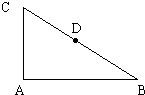 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,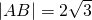 ,
,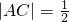 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C.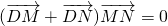 ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.