Question

已知双曲线C₁以点A（0，1）为顶点，且过点B(-

3

，2)．
（1）求双曲线C₁的标准方程；
（2）求离心率为

2

2

，且以双曲线C₁的焦距为短轴长的椭圆的标准方程；
（3）已知点P在以点A为焦点、坐标原点为顶点的抛物线C₂上运动，点M的坐标为（2，3），求PM+PA的最小值及此时点P的坐标．

Answer 1

分析：（1）双曲线C₁的一个顶点的坐标是（0，1），可确定双曲线的焦点在y轴上，又由过点B(-

3

，2)，从而可求双曲线的标准方程；
（2）由于椭圆以双曲线C₁的焦距为短轴长，可得到椭圆的短半轴长，再由椭圆的离心率即可得到长半轴长，进而得到椭圆的标准方程；
（3）利用抛物线的定义，将点到焦点距离转化为到准线的距离，利用三点共线，即可得到结论．

解答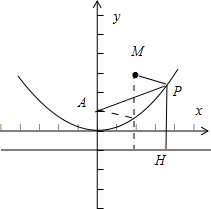：解：（1）由于双曲线C₁以点A（0，1）为顶点，
则双曲线的实半轴为1，方程可设为

y2

1

-

x2

b 2 1

=1(b1＞0)
将(-

3

，2)代入，得

b

2 1

=1
双曲线标准方程为：y²-x²=1；
（2）由（1）知，

c

2 1

=2，∴b=

2

，∴b²=2
∴e2=

c2

a2

=

a2-b2

a2

=

1

2

，∴a²=4
∴椭圆标准方程为：

x2

4

+

y2

2

=1或  

y2

4

+

x2

2

=1；
（3）依题意，抛物线标准方程为：x²=4y
设点P到准线y=-1的垂线段为PH，则PA=PH
∴（PM+PA）_min=（PM+PH）_min=4
此时，P（2，1）

点评：本题考查双曲线，椭圆，抛物线的标准方程，考查圆锥线的定义与性质，考查轨迹方程的求解，定位定量是关键．