题目内容
已知椭圆C1: 的左、右焦点分别为F1、F2,右顶点为A,离心率
的左、右焦点分别为F1、F2,右顶点为A,离心率
(1)设抛物线C2:y2=4x的准线与x轴交于F1,求椭圆的方程;
(2)设已知双曲线C3以椭圆C1的焦点为顶点,顶点为焦点,b是双曲线C3在第一象限上任意-点,问是否存在常数λ(λ>0),使∠BAF1=λ∠BF1A恒成立?若存在,求出λ的值;若不存在,请说明理由.
解:(1)因为抛物线C2的准线方程为x=-1,
所以椭圆C1的左焦点F1的坐标为F1(-1,0),所以椭圆的半焦距c=1,
又椭圆的离心率e= ,
,
所以a=2,b=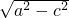 =
= ,
,
所以椭圆C1的方程为 ;
;
(2)存在常数λ=2,使∠BAF1=2∠BF1A恒成立,
证明如下:设椭圆的半焦距为c,
因为e= =
= ,所以a=2c,b=
,所以a=2c,b= c,
c,
所以双曲线C3的方程为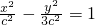 ,A(2c,0),
,A(2c,0),
设B(x0,y0)(x0>0,y0>0),则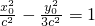 ,
,
①当AB⊥x轴时,x0=2c,y0=3c,则tan∠BF1A=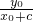 =
=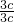 =1,
=1,
又∠BF1A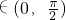 ,所以
,所以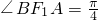 ,
,
所以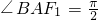 =2∠BF1A;
=2∠BF1A;
②当AB不与x轴垂直时,即x0≠2c时,
因为tan∠BAF1=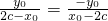 ,tan∠BF1A=
,tan∠BF1A=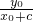 ,
,
所以tan2∠BF1A=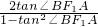 =
=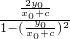 ,
,
又因为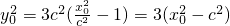 ,
,
所以tan2∠BF1A=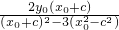 =
=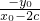 =tan∠BAF1,
=tan∠BAF1,
又∠BAF1与2∠BF1A同在(0, )或(
)或( ,π)内,
,π)内,
所以∠BAF1=2∠BF1A.
综上可知存在λ=2,使得∠BAF1=2∠BF1A恒成立.
分析:(1)由抛物线准线方程可得椭圆左焦点,从而得c值,再由离心率得a,由b=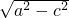 得b;
得b;
(2)可先通过垂直情况求出λ=2,然后作出一般证明.证明如下:设椭圆的半焦距为c,由离心率及双曲线与椭圆的关系可得双曲线C3的方程为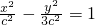 ,A(2c,0),设B(x0,y0)(x0>0,y0>0),①当AB⊥x轴时,易求
,A(2c,0),设B(x0,y0)(x0>0,y0>0),①当AB⊥x轴时,易求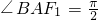 ,利用斜率公式可得tan∠BF1A,从而求得
,利用斜率公式可得tan∠BF1A,从而求得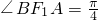 ,得证;②当AB不与x轴垂直时,即x0≠2c时,利用斜率公式表示出tan∠BF1A及tan∠BAF1,根据倍角公式可求证tan2∠BF1A=tan∠BAF1,再由∠BAF1与2∠BF1A的范围即可证得∠BAF1=2∠BF1A,综合①②可得结论;
,得证;②当AB不与x轴垂直时,即x0≠2c时,利用斜率公式表示出tan∠BF1A及tan∠BAF1,根据倍角公式可求证tan2∠BF1A=tan∠BAF1,再由∠BAF1与2∠BF1A的范围即可证得∠BAF1=2∠BF1A,综合①②可得结论;
点评:本题考查直线与圆锥曲线的位置关系、圆锥曲线的方程,考查直线的斜率公式,考查分类讨论思想,考查学生对问题的分析解决能力,先用特殊情况探求λ值,再作出一般证明是解决(2)问的关键.
所以椭圆C1的左焦点F1的坐标为F1(-1,0),所以椭圆的半焦距c=1,
又椭圆的离心率e=
 ,
,所以a=2,b=
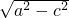 =
= ,
,所以椭圆C1的方程为
 ;
;(2)存在常数λ=2,使∠BAF1=2∠BF1A恒成立,
证明如下:设椭圆的半焦距为c,
因为e=
 =
= ,所以a=2c,b=
,所以a=2c,b= c,
c,所以双曲线C3的方程为
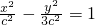 ,A(2c,0),
,A(2c,0),设B(x0,y0)(x0>0,y0>0),则
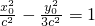 ,
,①当AB⊥x轴时,x0=2c,y0=3c,则tan∠BF1A=
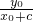 =
=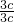 =1,
=1,又∠BF1A
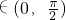 ,所以
,所以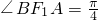 ,
,所以
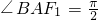 =2∠BF1A;
=2∠BF1A;②当AB不与x轴垂直时,即x0≠2c时,
因为tan∠BAF1=
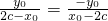 ,tan∠BF1A=
,tan∠BF1A=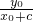 ,
,所以tan2∠BF1A=
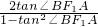 =
=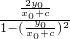 ,
,又因为
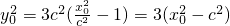 ,
,所以tan2∠BF1A=
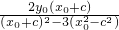 =
=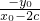 =tan∠BAF1,
=tan∠BAF1,又∠BAF1与2∠BF1A同在(0,
 )或(
)或( ,π)内,
,π)内,所以∠BAF1=2∠BF1A.
综上可知存在λ=2,使得∠BAF1=2∠BF1A恒成立.
分析:(1)由抛物线准线方程可得椭圆左焦点,从而得c值,再由离心率得a,由b=
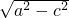 得b;
得b;(2)可先通过垂直情况求出λ=2,然后作出一般证明.证明如下:设椭圆的半焦距为c,由离心率及双曲线与椭圆的关系可得双曲线C3的方程为
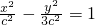 ,A(2c,0),设B(x0,y0)(x0>0,y0>0),①当AB⊥x轴时,易求
,A(2c,0),设B(x0,y0)(x0>0,y0>0),①当AB⊥x轴时,易求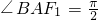 ,利用斜率公式可得tan∠BF1A,从而求得
,利用斜率公式可得tan∠BF1A,从而求得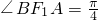 ,得证;②当AB不与x轴垂直时,即x0≠2c时,利用斜率公式表示出tan∠BF1A及tan∠BAF1,根据倍角公式可求证tan2∠BF1A=tan∠BAF1,再由∠BAF1与2∠BF1A的范围即可证得∠BAF1=2∠BF1A,综合①②可得结论;
,得证;②当AB不与x轴垂直时,即x0≠2c时,利用斜率公式表示出tan∠BF1A及tan∠BAF1,根据倍角公式可求证tan2∠BF1A=tan∠BAF1,再由∠BAF1与2∠BF1A的范围即可证得∠BAF1=2∠BF1A,综合①②可得结论;点评:本题考查直线与圆锥曲线的位置关系、圆锥曲线的方程,考查直线的斜率公式,考查分类讨论思想,考查学生对问题的分析解决能力,先用特殊情况探求λ值,再作出一般证明是解决(2)问的关键.

练习册系列答案
相关题目
 的左、右焦点分别为F1、F2,其中一个焦点和抛物线C:y2=2px(p>0)的焦点重合.
的左、右焦点分别为F1、F2,其中一个焦点和抛物线C:y2=2px(p>0)的焦点重合.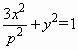 的左、右焦点分别为F1、F2,其中一个焦点和抛物线C:y2=2px(p>0)的焦点重合.
的左、右焦点分别为F1、F2,其中一个焦点和抛物线C:y2=2px(p>0)的焦点重合.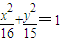 的左焦点为F,点P为椭圆上一动点,过点以F为圆心,1为半径的圆作切线PM,PN,其中切点为M,N则四边形PMFN面积的最大值 为 .
的左焦点为F,点P为椭圆上一动点,过点以F为圆心,1为半径的圆作切线PM,PN,其中切点为M,N则四边形PMFN面积的最大值 为 .