Question

【题目】设无穷数列的每一项均为正数，对于给定的正整数，()，若是等比数列，则称为数列.

（1）求证：若是无穷等比数列，则是数列；

（2）请你写出一个不是等比数列的数列的通项公式；

（3）设为数列，且满足，请用数学归纳法证明：是等比数列.

Answer 1

【答案】（1）证明见解析.（2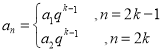）().(答案不唯一).（3）证明见解析

【解析】

（1）通过证明，证得数列是等比数列，由此证得为数列.

（2）根据满足的数列是等比数列，但无穷数列不是等比数列，举出相应的例子.

（3）首先根据已知条件得到，再利用数学归纳法证明（或者利用数学归纳法证明），由此证得是等比数列.

（1）设是公比为的等比数列，对于给定的正整数，()，

∴，，

又，∴是等比数列，

∴为数列.

（2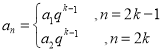）().(答案不唯一)

简洁的例子如：().

（3）∵为数列，∴是等比数列，其中()，

∴()，

∴()是常数列，设常数为，即()，

以下用数学归纳法证明(法一)()，

①由已知可得：当时命题成立；

②假设(，)时命题成立，即，，

当时，∵()是常数列，

∴(，)，

∴，

等式也成立.

根据①和②可以断定，对任何都成立，即是等比数列.

令，以下用数学归纳法证明(法二)()，

①∵，∴，∴，∴，即，

∴当时命题成立，

假设(，)时命题成立，即()；

②当时，，

等式也成立；

根据①和②可以断定，对任何都成立，即是等比数列.