题目内容
命题“对
 ,都有
,都有 ”的否定为( )
”的否定为( )
A.对  ,都有 ,都有 | B.不存在 ,都有 ,都有 |
C.  ,使得 ,使得 | D.  ,使得 ,使得 |
D
解析试题分析:全称命题的否定,只需要将任意换为存在,对结论进行否定即可.
考点:全称命题的否定.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若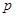 是
是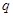 的必要条件,
的必要条件,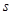 是
是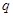 的充分条件,那么下列推理一定正确的是( )
的充分条件,那么下列推理一定正确的是( )
A.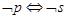 | B.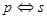 | C.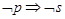 | D.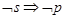 |
已知命题p:?x∈[0, ],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
A.[- ,-1] ,-1] |
B.[- ,2] ,2] |
| C.[-1,2] |
D.[- ,+∞) ,+∞) |
已知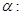 “
“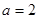 ”;
”;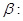 “直线
“直线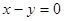 与圆
与圆 相切”.则
相切”.则 是
是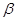 的( )
的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
已知向量 ,
,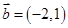 ,则
,则 的充要条件是( )
的充要条件是( )
A. | B. | C. | D. |
“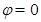 ”是“函数
”是“函数 为奇函数”的( )
为奇函数”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.非充分非必要条件 |
“ ”是“
”是“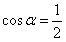 ”的( )
”的( )
| A.必要不充分条件 |
| B.充分不必要条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
已知命题
 ,
, ;命题
;命题
 ,
, ,则下列命题中为真命题的是:( )
,则下列命题中为真命题的是:( )
A. |
B. |
C. |
D. |
 .函数
.函数 为
为 上可导函数,则
上可导函数,则 是
是 为函数
为函数 极值点的充要条件.
极值点的充要条件. .命题“
.命题“ ”的否定是“
”的否定是“ ”.
”. .命题“在
.命题“在 中,若
中,若 ”的逆命题为假命题.
”的逆命题为假命题. .“
.“ ”是“函数
”是“函数 是偶函数”的充要条件.
是偶函数”的充要条件.