题目内容

10．作出函数f（x）=$\sqrt{{x}^{2}-6x+9}$+$\sqrt{{x}^{2}+6x+9}$的图象，并指出f（x）的单调区间．

分析 原函数化为f（x）=|x-3|+|x+3|=$\left\{\begin{array}{l}{2x，x＞3}\\{6，-3≤x≤3}\\{-2x，x＜-3}\end{array}\right.$，画图即可．

解答 解：f（x）=$\sqrt{{x}^{2}-6x+9}$+$\sqrt{{x}^{2}+6x+9}$=|x-3|+|x+3|=$\left\{\begin{array}{l}{2x，x＞3}\\{6，-3≤x≤3}\\{-2x，x＜-3}\end{array}\right.$，
其图象如图所示：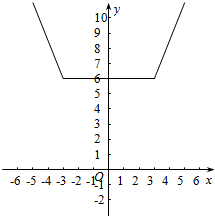

由图象可知，f（x）在（-∞，-3）上单调递减，在（3，+∞）上单调递增．

点评 本题考查了函数图象的画法，关键是化为分段函数，属于基础题．

练习册系列答案
相关题目
20．等差数列{an}中，已知公差d=2，前n项和为Sn，且S1，S2，S4成等比数列．
（1）求{an}的通项公式；
（2）设bn=$（-1）^{n}\frac{4n}{{a}_{n}•{a}_{n+1}}$，求{bn}的前n项和Tn．
1．函数y=$\frac{{e}^{x}+{e}^{-x}}{{e}^{x}-{e}^{-x}}$（x≥ln2）的最大值为$\frac{5}{3}$．
18．给出下列判断：①若存在x1，x2∈I，当x1＜x2时，f（x1）＜f（x2）则y=f（x）在I上是增函数；②函数y=$\frac{1}{x}$在定义域内是减函数；③y=（x-1）2在（0，+∞）上是增函数；④y=-$\frac{1}{x}$在（-∞，0）上为增函数；其中错误的个数有（　　）
A．1B．2C．3D．4
5．F为抛物线C：y2=8x的焦点，P（x1，y1）为抛物线C上一点，若|FP|=3，则x1=（　　）
A．1B．5C．1或5D．1或-5
15．函数f（x）=lg[-x2+（3a+2）x-3a-1]的定义域为集合A．
（1）设函数y=x2-2x+3（0≤x≤3）的值域为集合B，若A∩B=B，求实数a的取值范围；
（2）设集合B={x|（x-2a）（x-a2-1）＜0}，是否存在实数a，使得A=B？若存在，求出a的值；若不存在，请说明理由．
2．命题?x0∈（-1，1），x02-a＞0的否定为?x∈（-1，1），x2-a≤0．．
19．已知：a，b∈R，ab=2．则1，ab，$\frac{{a}^{2}+{b}^{2}}{2}$的大小关系为$\frac{{a}^{2}{+b}^{2}}{2}$≥ab＞1．
20．θ∈（-$\frac{π}{2}$，$\frac{π}{2}$），则3${\;}^{1-lo{g}_{3}cosθ}$=$\frac{3}{cosθ}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网