题目内容
一个数列{an}:当n为奇数时,an=5n+1;当n为偶数时, 求这个数列的前2m项的和(m是正整数).
求这个数列的前2m项的和(m是正整数).
【答案】分析:由题意分析得出这个数列的奇数项是等差数列,偶数项是等比数列,再利用分组求和法求出S2m
解答:解:因为a2k+1-a2k-1=[5(2k+1)+1]-[5(2k-1)+1]=10,
所以a1,a3,a5,a2m-1是公差为10的等差数列
因为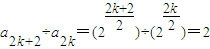 ,
,
所以a2,a4,a6,a2m是公比为2的等比数列
从而数列{an}的前2m项和为:S2m=(a1+a3+a5+…+a2m-1)+(a2+a4+a6+…+a2m)= +
+
=5m2+m+2m+1-2.
点评:本题考查了分段数列及分组求和的相关知识点,属于典型题型,常规方法的考查.
解答:解:因为a2k+1-a2k-1=[5(2k+1)+1]-[5(2k-1)+1]=10,
所以a1,a3,a5,a2m-1是公差为10的等差数列
因为
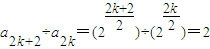 ,
,所以a2,a4,a6,a2m是公比为2的等比数列
从而数列{an}的前2m项和为:S2m=(a1+a3+a5+…+a2m-1)+(a2+a4+a6+…+a2m)=
 +
+
=5m2+m+2m+1-2.
点评:本题考查了分段数列及分组求和的相关知识点,属于典型题型,常规方法的考查.

练习册系列答案
相关题目