题目内容
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,AC与BD交于点O,PO⊥平面ABCD,E为CD的中点连接AE交BD于G,点F在侧棱PD上,且DF![]() PD.
PD.
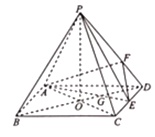
(1)求证:PB∥平面AEF;
(2)若![]() ,求三棱锥E﹣PAD的体积.
,求三棱锥E﹣PAD的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法证明
轴,建立空间直角坐标系,利用向量法证明![]() 平面
平面![]() ;
;
(2)求出![]() ,
,![]() ,由
,由![]() ,求出
,求出![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,由此能求出结果.
,由此能求出结果.
(1)证明:四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平面
平面![]() ,
,
![]() 为
为![]() 的中点连接
的中点连接![]() 交
交![]() 于
于![]() ,点
,点![]() 在侧棱
在侧棱![]() 上,且
上,且![]() ,
,
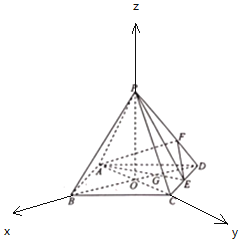
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则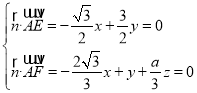 ,取
,取![]() ,得
,得![]() ,
,
![]()
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;
(2)解:![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() ,
,
三棱锥![]() 的体积:
的体积:
![]()
![]()
![]()
![]() .
.

【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.


【题目】为了节能减排,发展低碳经济,我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表 | ||||
新能源汽车生产情况 | 新能源汽车销售情况 | |||
产品(万辆) | 比上年同期 | 销量(万辆) | 比上年同期 | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |
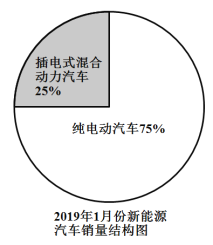
根据上述图表信息,下列结论错误的是( )
A.2017年3月份我国新能源汽车的产量不超过![]() 万辆
万辆
B.2017年我国新能源汽车总销量超过![]() 万辆
万辆
C.2018年8月份我国新能源汽车的销量高于产量
D.2019年1月份我国插电式混合动力汽车的销量低于![]() 万辆
万辆