题目内容
【题目】已知圆
的圆心在直线
上，且与直线
相切于点
.
（1）求圆方程；
（2）是否存在过点
的直线
与圆交于
两点，且
的面积是
（
为坐标原点），若存在，求出直线的方程，若不存在，请说明理由.
【答案】（1）
；（2）
．
【解析】试题分析：
（1）求圆的方程，由于圆心在直线
上，因此可设圆心坐标为
，同时设圆半径为
，由圆与直线相切，从而圆心到直线
的距离等于圆的半径以及圆心到切点的距离也是半径列出方程组解得
得圆标准方程；（2）此类问题是假设直线存在，然后可分直线的斜率存在和不存在两种情形讨论，斜率存在时，设直线方程为
，求出圆心到直线的距离
，再由勾股定理得弦长
，由面积得关于
的方程，求出
（如无解说明此种情况不存在）；当斜率不存在时直线方程为
，直接验证即可．
试题解析：
（1）设圆心坐标为
，则圆的方程为： 
，又与
相切，则有
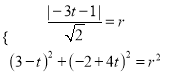，解得： 
， 
，所以圆的方程为： 
；
（2）由题意得：当
存在时，设直线
，设圆心到直线的距离为
，
则有
，进而可得：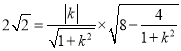 
化简得： 
，无解；
当
不存在时， 
，则圆心到直线的距离
，那么
， 
，满足题意，所以直线
的方程为： 
.
【题目】继共享单车之后，又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市，一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”，每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”，李先生家离上班地点10公里，每天租用共享汽车上下班，由于堵车因素，每次路上开车花费的时间是一个随机变量，根据一段时间统计40次路上开车花费时间在各时间段内的情况如下：
时间（分钟） |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率，假设每次路上开车花费的时间视为用车时间，范围为
分钟.
（Ⅰ）若李先生上.下班时租用一次共享汽车路上开车不超过45分钟，便是所有可选择的交通工具中的一次最优选择，设
是4次使用共享汽车中最优选择的次数，求
的分布列和期望.
（Ⅱ）若李先生每天上下班使用共享汽车2次，一个月（以20天计算）平均用车费用大约是多少（同一时段，用该区间的中点值作代表）.
