题目内容
如图,在直角三角形ABC中,AD是斜边BC上的高,有很多大家熟悉的性质,例如“AB⊥AC”,勾股定理“|AB|2+|AC|2=|BC|2”和“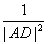 =
=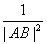 +
+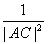 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
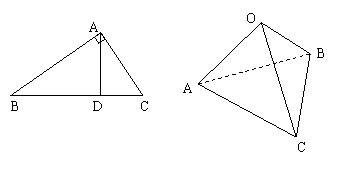 |
解:(以下仅供参考,不同结论请酌情给分。每个正确结论给2分,证明给5分) 可以得出有以下结论:
(Ⅰ)三个侧面OAB、OAC、OBC两两互相垂直(或OA⊥BC、OB⊥AC、OC⊥AB)
(Ⅱ)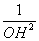 =
=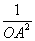 +
+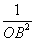 +
+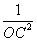 (H为ΔABC的重心)
(H为ΔABC的重心)
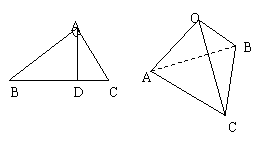 (Ⅲ)
(Ⅲ) +
+ +
+ =
=
以下给出具体的证明:
(1)证明:∵OA⊥OC,OB⊥OC ∴OC⊥平面OAB
∴平面OAC⊥平面OAB 平面OBC⊥平面OAB 同理可证平面OBC⊥平面OAC
(2)证明:如图二 连接AH并延长AH交BC于D连接OD
∵OA⊥面OBC∴OA⊥OD
在RtΔABC中 ∵OH⊥OD ∴OH·AD=AO·OD
 ∴OH2·AD2=AO2·OD2
∴OH2·AD2=AO2·OD2
又∵AD2=
OA2+ OD2 ∴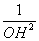 =
=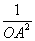 +
+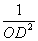
∵AD⊥BC,由三垂线定理得:BC⊥OD
∴在RtΔOBC中 OD2 ·BC2 =BO2·CO2
∴OD2=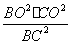 又∵BC2= BO2+CO2
又∵BC2= BO2+CO2
∴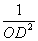 =
=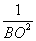 +
+ ② 由①②得:
② 由①②得: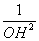 =
=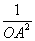 +
+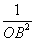 +
+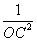
(Ⅳ) 证明:如图二(延用(Ⅸ)中的字母a,b,c)∵H为垂心 ∴AD⊥BC
又∵OA、OB、OC两两垂直 ∴SΔOAB=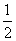 ab SΔOBC=
ab SΔOBC=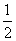 bc
SΔOAC=
bc
SΔOAC=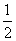 ac
ac
SΔABC=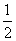 BC·AD
BC·AD
∴ +
+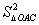 +
+ =
= (
a2 b2+ b2 c2+ a2 c2)=
(
a2 b2+ b2 c2+ a2 c2)=  a2(b2+ c2)+
a2(b2+ c2)+ b2 c2…………①
b2 c2…………①
又∵在RtΔBOC中,OD⊥BC ∴OB2·OC2= b2 c2=OD2·BC2=OD2·(b2+ c2)………②
∴②代入①得: +
+ +
+ =
= (b2+ c2)·AD2=
(b2+ c2)·AD2= BC2·AD2=
BC2·AD2=

 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点, 如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S
如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S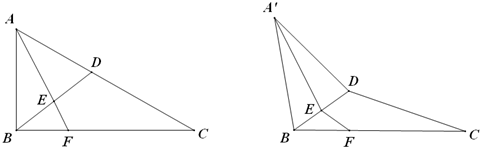
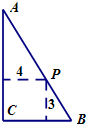 (2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )
(2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )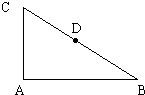 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,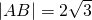 ,
,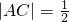 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C.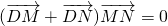 ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.