题目内容
)设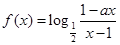 为奇函数,
为奇函数,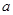 为常数.
为常数.
(1)求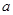 的值;
的值;
(2)判断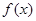 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;
(3)若对于区间 [3,4]上的每一个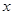 的值,不等式
的值,不等式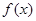 >
>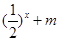 恒成立,求实数
恒成立,求实数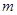 的取值范围.
的取值范围.
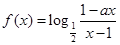 为奇函数,
为奇函数,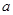 为常数.
为常数.(1)求
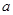 的值;
的值;(2)判断
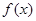 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;(3)若对于区间 [3,4]上的每一个
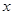 的值,不等式
的值,不等式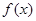 >
>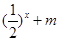 恒成立,求实数
恒成立,求实数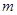 的取值范围.
的取值范围.(1)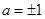 (2)在(1,+∞)上是增函数(3)
(2)在(1,+∞)上是增函数(3)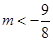
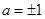 (2)在(1,+∞)上是增函数(3)
(2)在(1,+∞)上是增函数(3)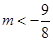
试题分析:解:(1)∵
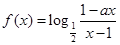 为奇函数,
为奇函数,∴
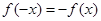 对于
对于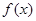 定义域中任意实数恒成立,
定义域中任意实数恒成立,即
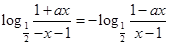 2分
2分∴
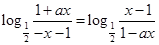 ∴
∴ ∴
∴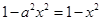
∴
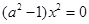 对于
对于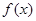 定义域中任意实数恒成立
定义域中任意实数恒成立∵
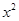 不恒为0,∴
不恒为0,∴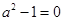 ∴
∴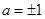 4分
4分当
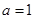 时
时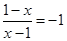 不符题意
不符题意∴
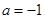 5分
5分(2)由(1)得
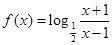
设1<x1<x2,则
f(x1)-f(x2)=log
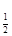
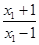 -log
-log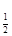
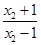 =log
=log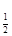
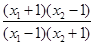
=log
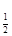
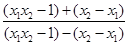 7分
7分∵ 1<x1<x2,∴ x2-x1>0,
∴ (x1x2-1)+(x2-x1)>(x1x2-1)-(x2-x1)>0
即
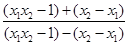 >1. 9分
>1. 9分∴ f(x1)-f(x2)<0即f(x1)<f(x2),在(1,+∞)上是增函数 10分
(3)由(1),不等式
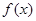 >
>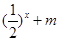 可化为
可化为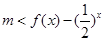 ,即
,即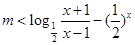
由题意得对于区间[3,4]上的每一个
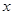 的值,
的值,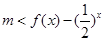 恒成立 2分
恒成立 2分令
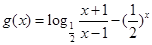 ,则
,则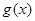 区间[3,4]上为增函数
区间[3,4]上为增函数∵
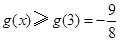 ∴
∴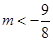 15分
15分点评:解决的关键是对于函数奇偶性和单调性的灵活运用,以及利用分离参数的思想求解函数的最值得到范围。属于中档题。

练习册系列答案
相关题目
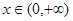 时,幂函数
时,幂函数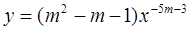 为减函数,求实数
为减函数,求实数 的值。
的值。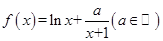
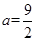 时,如果函数
时,如果函数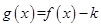 仅有一个零点,求实数
仅有一个零点,求实数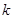 的取值范围.
的取值范围.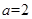 时,比较
时,比较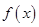 与1的大小.
与1的大小.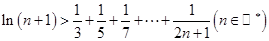
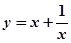 在
在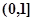 上是减函数,在
上是减函数,在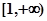 上是增函数;
上是增函数;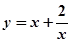 在
在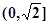 上是减函数,在
上是减函数,在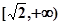 上是增函数;
上是增函数;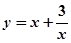 在
在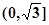 上是减函数,在
上是减函数,在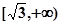 上是增函数;
上是增函数;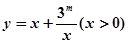 的值域是
的值域是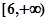 ,则实数
,则实数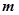 的值是 .
的值是 .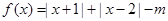
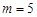 时,求
时,求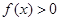 的解集
的解集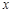 的不等式
的不等式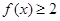 的解集是
的解集是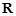 ,求
,求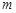 的取值范围
的取值范围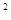 -2s) ≥-f(2t-t
-2s) ≥-f(2t-t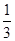 )的值;
)的值; ,(1)分别求
,(1)分别求 ;(2)然后归纳猜想一般性结论,并给出证明.
;(2)然后归纳猜想一般性结论,并给出证明.  .
. ,函数
,函数 是R上的奇函数,当
是R上的奇函数,当 时
时 ,(i)求实数
,(i)求实数 与
与
 时,求
时,求 的两根中,一根属于区间
的两根中,一根属于区间 ,另一根属于区间
,另一根属于区间 ,求实数
,求实数