题目内容
已知函数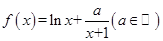
(1)当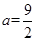 时,如果函数
时,如果函数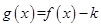 仅有一个零点,求实数
仅有一个零点,求实数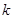 的取值范围.
的取值范围.
(2)当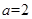 时,比较
时,比较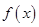 与1的大小.
与1的大小.
(3)求证: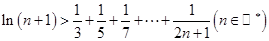
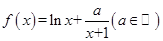
(1)当
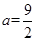 时,如果函数
时,如果函数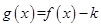 仅有一个零点,求实数
仅有一个零点,求实数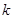 的取值范围.
的取值范围.(2)当
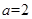 时,比较
时,比较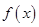 与1的大小.
与1的大小.(3)求证:
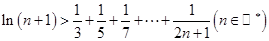
(1)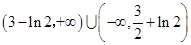
(2)①当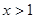 时,
时,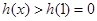 ,即
,即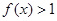 ;
;
②当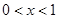 时,
时,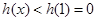 ,即
,即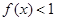 ;
;
③当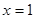 时,
时,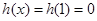 ,即
,即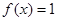
(3)利用(2)的结论或数学归纳法证明
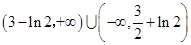
(2)①当
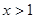 时,
时,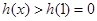 ,即
,即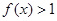 ;
;②当
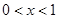 时,
时,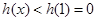 ,即
,即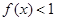 ;
;③当
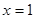 时,
时,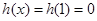 ,即
,即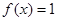
(3)利用(2)的结论或数学归纳法证明
试题分析:(1)当
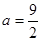 时,
时,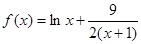 ,定义域是
,定义域是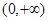 , 1分
, 1分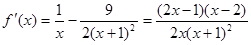 ,
,令
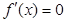 ,得
,得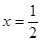 或
或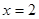 . 2分
. 2分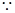 当
当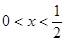 或
或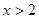 时,
时,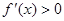 ,当
,当 时,
时,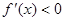 ,
, 函数
函数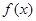 在
在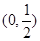 、
、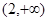 上单调递增,在
上单调递增,在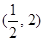 上单调递减. 4分
上单调递减. 4分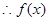 的极大值是
的极大值是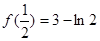 ,极小值是
,极小值是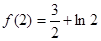 .
.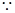 当
当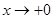 时,
时,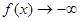 ;当
;当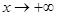 时,
时,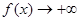 ,
,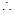 当
当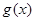 仅有一个零点时,
仅有一个零点时,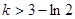 或
或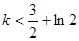 .
.∴
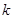 的取值范围是
的取值范围是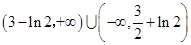 5分
5分(2)当
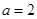 时,
时,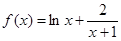 ,定义域为
,定义域为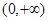 .
.令
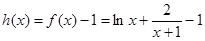 ,
,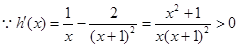 ,
,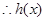 在
在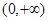 上是增函数. 7分
上是增函数. 7分∵
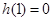
∴①当
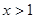 时,
时,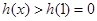 ,即
,即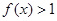 ;
;②当
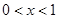 时,
时,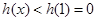 ,即
,即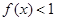 ;
;③当
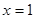 时,
时,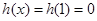 ,即
,即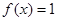 . 9分
. 9分(3)(法一)根据(2)的结论,当
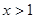 时,
时,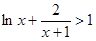 ,即
,即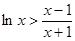 .
.令
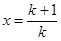 ,则有
,则有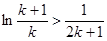 ,
, 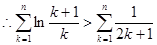 . 12分
. 12分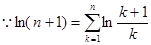 ,
,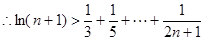 . 14分
. 14分(法二)①当
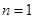 时,
时,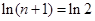 .
.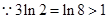 ,
,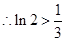 ,即
,即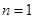 时命题成立. 10分
时命题成立. 10分②假设
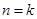 时,命题成立,即
时,命题成立,即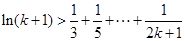 .
.则当
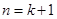 时,
时,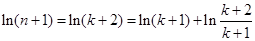
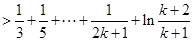 .
.根据(2)的结论,当
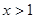 时,
时,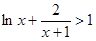 ,即
,即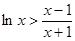 .
.令
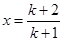 ,则有
,则有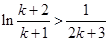 ,
,则有
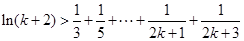 ,即
,即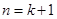 时命题也成立. 13分
时命题也成立. 13分因此,由①②知不等式成立. 14分
点评:导数是研究函数性质的有力工具,要灵活运用解决问题,利用数学归纳法证明不等式时要注意放缩不等式的应用.

练习册系列答案
相关题目
 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得). 的解析式及其定义域;
的解析式及其定义域;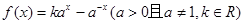 ,
,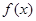 是定义域为R上的奇函数.
是定义域为R上的奇函数.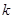 的值,并证明当
的值,并证明当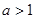 时,函数
时,函数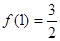 ,函数
,函数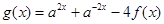 ,
,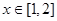 ,求
,求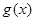 的值域;
的值域;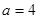 ,试问是否存在正整数
,试问是否存在正整数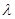 ,使得
,使得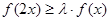 对
对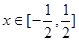 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ( )
( )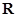 上是单调增函数
上是单调增函数 时,有不等式( )
时,有不等式( )
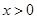 时
时 时
时
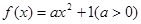 ,
,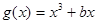
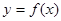 与曲线
与曲线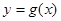 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求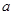 ,
,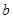 的值;
的值;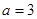 ,
,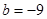 时,若函数
时,若函数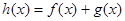 在区间[
在区间[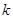 ,2]上的最大值为28,求
,2]上的最大值为28,求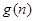 与科技成本的投入次数
与科技成本的投入次数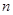 的关系是
的关系是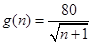 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第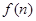 万元.
万元.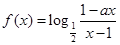 为奇函数,
为奇函数,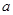 为常数.
为常数.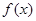 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;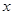 的值,不等式
的值,不等式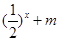 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.