题目内容
(本小题满分12分)已知函数f(x)=kx3-3(k+1)x2-2k2+4,若f(x)的单调减区间为(0,4 ).
).
(1)求k的值;
(2)对任意的t∈[-1,1],关于x的方程2x2+5x+a=f(t)总有实根,求实数a的取值范围.
解:(1)f′(x)=3kx2-6(k+1)x,
又∵f′(4)=0,∴k=1.
(2)由(1)得f(x)=x3-6x2+2,
∴f′(t)=3t2-12t.
∵当-1<t<0时,f′(t)>0;当0<t<1时,f′(t)<0,且f(-1)=-5,f(1)=-3,
∴f(t)≥-5.
∵2x2+5x+a≥ ,
,
∴ ≤-5,解得a≤-
≤-5,解得a≤- .
.
解析

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知f'(0)=2,则
 =( )
=( )
| A.4 | B.-8 | C.0 | D.8 |
将函数 的图象沿x轴方向左平移
的图象沿x轴方向左平移 个单位, 则平移后的图象所对应函数的解析式是
个单位, 则平移后的图象所对应函数的解析式是
A. | B. |
C. | D. |

 时,求函数
时,求函数 的单调区间;
的单调区间;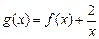 在
在 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围. (
( 且
且 ).
). 时,求证:函数
时,求证:函数 在
在 上单调递
上单调递 增;
增; 有三个零点,求t的值;
有三个零点,求t的值; ,试求a的取值范围.
,试求a的取值范围. .
.  处取到极值?若有可能,求实数
处取到极值?若有可能,求实数 的值;否则说明理由;
的值;否则说明理由; 上为增函数,求实数
上为增函数,求实数 ,Q=
,Q= t.今该公司将5
t.今该公司将5 是直线
是直线 上三点,向量
上三点,向量 满足:
满足: ,且函数
,且函数 定义域内可导。
定义域内可导。 ,证明:
,证明: ;
; 对
对 及
及 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。 为自然对数的底数
为自然对数的底数
 时,求函数
时,求函数 的极值;
的极值; 的取值范围.
的取值范围.