题目内容
斜三棱柱ABC—A′B′C′的底面是正三角形,且C′B=C′C.
(1)证明:AC′⊥BC;
(2)若侧面BCC′B′垂直于底面,侧棱长为3,底棱长为2,求两底面间的距离.
(1)证明:AC′⊥BC;
(2)若侧面BCC′B′垂直于底面,侧棱长为3,底棱长为2,求两底面间的距离.
(1)证明见解析。
(2)
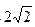
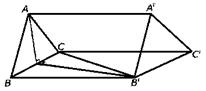
(1)取BC中点O,则AB=AC?AO⊥BC.BC′=CC′?C′O⊥BC.
∴BC⊥面AOC′?BC⊥AC′
(2)面BB′C′C⊥面ABC
∴AO⊥面BB′C′C C′O⊥底面ABC,
面ABC∥面A′B′C′
∴OC′为两平面间的距离,
OC′为所求.
∵BC="AC=AB=2 " ∴CO="1 " CC′="3 " ∴OC′=


练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 与
与
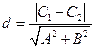 .
.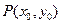 到直线
到直线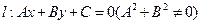 的有向距离为
的有向距离为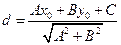 .已知点
.已知点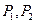 到直线
到直线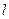 的有向距离分别是
的有向距离分别是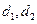 ,给出以下命题:
,给出以下命题: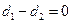 ,则直线
,则直线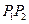 与直线
与直线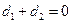 ,则直线
,则直线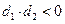 ,则直线
,则直线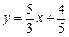 的距离中的最小值是
的距离中的最小值是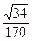
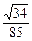


 的高
的高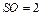 ,底边长
,底边长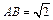 .求异面直线
.求异面直线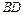 和
和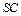 之间的距离.
之间的距离.


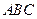 的边长为
的边长为 ,沿平行于
,沿平行于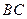 的线段
的线段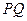 折起,使平面
折起,使平面 平面
平面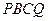 ,设点
,设点 到直线
到直线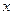 ,
,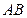 的长为
的长为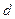 .
.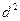 取得最小值,最小值是多少;
取得最小值,最小值是多少;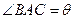 ,求
,求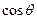 的最小值.
的最小值.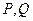 分别为直线
分别为直线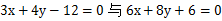 上任一点,则
上任一点,则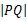 的最小值为 。
的最小值为 。