题目内容
已知点A(2,0),B(0,2),C(cosα,sinα),且0<α<π.
(1)若 ,求sin2α的值;
,求sin2α的值;
(2)若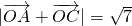 ,求
,求 与
与 的夹角.
的夹角.
解:(1)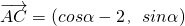 ,
,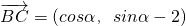 ,∵
,∵ ,∴
,∴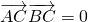 ,
,
∴ ,∴
,∴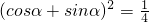 ,∴
,∴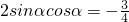 ,∴
,∴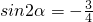 .
.
(2)由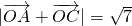 得 (2+cosα)2+sin2α=7,∴
得 (2+cosα)2+sin2α=7,∴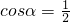 ,
,
又α∈(0,π),∴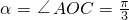 ,又
,又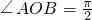 ,∴
,∴ 与
与 的夹角为
的夹角为 .
.
分析:(1)根据两个向量的数量积公式,两个向量垂直的性质,得到 ,平方可以求得sin2α的值.
,平方可以求得sin2α的值.
(2)由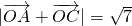 得 (2+cosα)2+sin2α=7,求得
得 (2+cosα)2+sin2α=7,求得 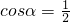 ,再根据α的范围求出α的值,从而求得
,再根据α的范围求出α的值,从而求得
 与
与 的夹角.
的夹角.
点评:本题考查三角函数的恒等变换及化简求值,两个向量的数量积公式,两个向量垂直的性质,求向量的模的方法,根据三角函数的值求角,求得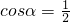 ,是解题的关键.
,是解题的关键.
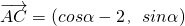 ,
,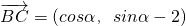 ,∵
,∵ ,∴
,∴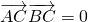 ,
,∴
 ,∴
,∴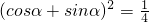 ,∴
,∴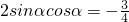 ,∴
,∴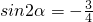 .
.(2)由
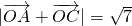 得 (2+cosα)2+sin2α=7,∴
得 (2+cosα)2+sin2α=7,∴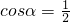 ,
,又α∈(0,π),∴
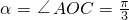 ,又
,又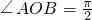 ,∴
,∴ 与
与 的夹角为
的夹角为 .
.分析:(1)根据两个向量的数量积公式,两个向量垂直的性质,得到
 ,平方可以求得sin2α的值.
,平方可以求得sin2α的值.(2)由
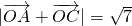 得 (2+cosα)2+sin2α=7,求得
得 (2+cosα)2+sin2α=7,求得 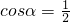 ,再根据α的范围求出α的值,从而求得
,再根据α的范围求出α的值,从而求得 与
与 的夹角.
的夹角.点评:本题考查三角函数的恒等变换及化简求值,两个向量的数量积公式,两个向量垂直的性质,求向量的模的方法,根据三角函数的值求角,求得
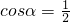 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目