题目内容
在△ABC中,若|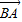 +
+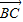 |=|
|=|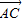 |,则△ABC一定是( )
|,则△ABC一定是( )A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.不能确定
【答案】分析:由|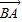 +
+ |=|
|=|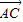 |,我们两边平方后,根据向量数量积的运算性质可得c2+a2+2cacosB=b2,结合余弦定理c2+a2-2cacosB=b2,我们可得cosB=0,结合B为△ABC的内角,我们易求出B的大小,进而判断三角形的形状.
|,我们两边平方后,根据向量数量积的运算性质可得c2+a2+2cacosB=b2,结合余弦定理c2+a2-2cacosB=b2,我们可得cosB=0,结合B为△ABC的内角,我们易求出B的大小,进而判断三角形的形状.
解答:解:∵|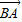 +
+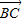 |=|
|=|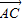 |,
|,
∴|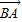 +
+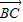 |2=|
|2=|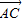 |2,
|2,
∴|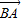 |2+|
|2+|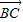 |2+2
|2+2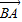 •
•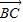 =|
=|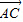 |2,
|2,
即c2+a2+2cacosB=b2
由余弦定理c2+a2-2cacosB=b2
得cosB=0
即B=90°
故△ABC一定是直角三角形
故选B
点评:本题考查的知识点是向量的模,余弦定理,根据向量模相等,则两个向量的平方相等,构造方程是解答的关键.
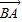 +
+ |=|
|=|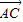 |,我们两边平方后,根据向量数量积的运算性质可得c2+a2+2cacosB=b2,结合余弦定理c2+a2-2cacosB=b2,我们可得cosB=0,结合B为△ABC的内角,我们易求出B的大小,进而判断三角形的形状.
|,我们两边平方后,根据向量数量积的运算性质可得c2+a2+2cacosB=b2,结合余弦定理c2+a2-2cacosB=b2,我们可得cosB=0,结合B为△ABC的内角,我们易求出B的大小,进而判断三角形的形状.解答:解:∵|
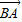 +
+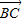 |=|
|=|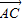 |,
|,∴|
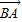 +
+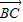 |2=|
|2=|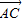 |2,
|2,∴|
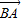 |2+|
|2+|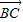 |2+2
|2+2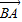 •
•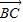 =|
=|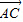 |2,
|2,即c2+a2+2cacosB=b2
由余弦定理c2+a2-2cacosB=b2
得cosB=0
即B=90°
故△ABC一定是直角三角形
故选B
点评:本题考查的知识点是向量的模,余弦定理,根据向量模相等,则两个向量的平方相等,构造方程是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,若acosA=bcosB,则△ABC的形状是( )
| A、等腰三角形 | B、直角三角形 | C、等腰直角三角形 | D、等腰或直角三角形 |
在△ABC中,若sinB=
,cosC=
,则cosA的值是( )
| 4 |
| 5 |
| 12 |
| 13 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|