题目内容
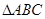 中,角
中,角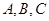 的对边分别为
的对边分别为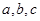 .已知
.已知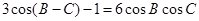 .
.(I)求
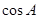 ;
;(II)若
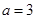 ,
,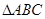 的面积为
的面积为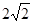 ,且
,且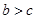 ,求
,求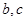 .
.(I)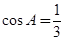 ;(II)
;(II)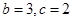 .
.
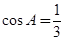 ;(II)
;(II)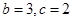 .
.试题分析:(I)在
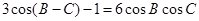 中,有差角
中,有差角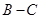 ,有单角
,有单角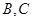 ,所以应将
,所以应将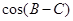 展开,将角统一为单角.
展开,将角统一为单角.由
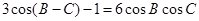 得:
得: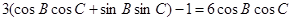 ,
,再移项合并得:
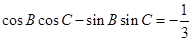 ,这样可得
,这样可得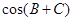 的值,从而求出
的值,从而求出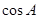 的值.
的值.(II)面积公式用哪一个?因为由(I)可得
 ,所以用
,所以用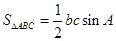 ,由此可得
,由此可得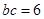 …①
…①为了求出
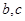 ,显然还应该再找一个含
,显然还应该再找一个含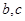 的等式.
的等式.因为已知
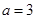 ,在(I)题中又求出了
,在(I)题中又求出了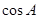 ,所以可用余弦定理再得一个含
,所以可用余弦定理再得一个含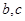 的等式:
的等式: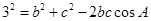 ……………………………………………②
……………………………………………②这样联立①②便可求出
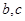 的值.
的值.试题解析:(I)
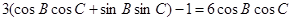 ,
,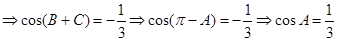 .
.(II)由(I)得
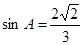 ,由面积
,由面积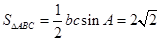 可得:
可得: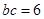 ………………①
………………①因为
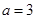 ,所以由余弦定理得:
,所以由余弦定理得: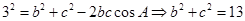 ………………………②
………………………②联立①②得
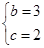 或
或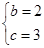 (舍).
(舍).综上:
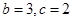 .
.
练习册系列答案
相关题目
 .
. 最大值和最小正周期;
最大值和最小正周期; 内角
内角 所对的边分别为
所对的边分别为 ,且
,且 .若
.若 ,求
,求 的值.
的值. 中
中 ,
,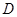 为线段
为线段 上一点,且
上一点,且 ,线段
,线段 .
.
 ,
, ,试求线段
,试求线段 的长.
的长.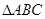 中,
中,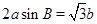 ,
, 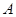 的大小;
的大小;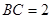 时,求
时,求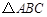 中,角
中,角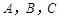 所对的边分别为
所对的边分别为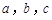 ,设
,设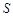 为
为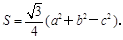
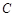 的大小;
的大小;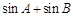 的最大值.
的最大值.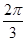 ,△ABC的面积S=
,△ABC的面积S= ,则AB=
,则AB= B. 90
B. 90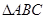 中,已知
中,已知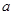 、
、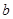 、
、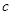 分别为
分别为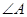 、
、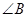 、
、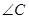 所对的边,
所对的边,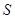 为
为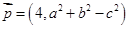 ,
,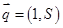 满足
满足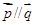 ,则
,则 .
.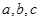 为
为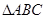 的三个内角
的三个内角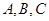 的对边,满足
的对边,满足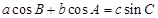 ,向量
,向量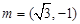 ,
,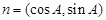 . 若
. 若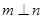 ,则角
,则角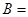 ___________.
___________.