题目内容
在锐角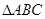 中,
中,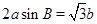 ,
,
(Ⅰ)求角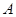 的大小;
的大小;
(Ⅱ)当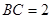 时,求
时,求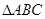 面积的最大值.
面积的最大值.
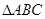 中,
中,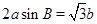 ,
, (Ⅰ)求角
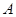 的大小;
的大小;(Ⅱ)当
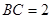 时,求
时,求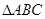 面积的最大值.
面积的最大值.(Ⅰ)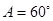 ;(Ⅱ)
;(Ⅱ)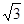 .
.
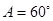 ;(Ⅱ)
;(Ⅱ)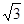 .
.试题分析:(Ⅰ)本小题考查正弦定理
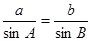 的边角转化,可求得
的边角转化,可求得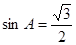 ,因为
,因为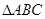 为锐角三角形,所以
为锐角三角形,所以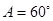 ;
;(Ⅱ)本小题首先利用余弦定理建立边角关系
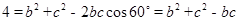 ,然后利用基本不等式得到
,然后利用基本不等式得到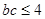 ,代入面积公式中可得
,代入面积公式中可得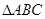 面积的最大值为
面积的最大值为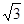 .
.试题解析:(Ⅰ)
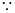
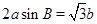 ,
,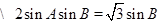 , 2分
, 2分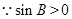 ,
, 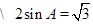
故
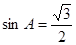 , 5分
, 5分因为
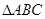 为锐角三角形,所以
为锐角三角形,所以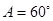 7分
7分(Ⅱ)设角
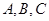 所对的边分别为
所对的边分别为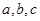 .
.由题意知
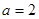 ,
,由余弦定理得
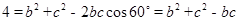 9分
9分又
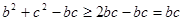 ,
,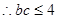 11分
11分
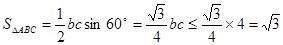 , 13分
, 13分当且且当
 为等边三角形时取等号,
为等边三角形时取等号,所以
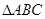 面积的最大值为
面积的最大值为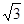 . 14分
. 14分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
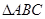 中,
中,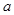 ,
,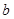 ,
,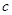 分别是角
分别是角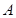 ,
,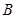 ,
,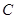 的对边,向量
的对边,向量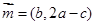 ,
,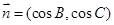 ,且
,且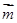 //
//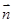 .
.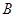 的大小;
的大小;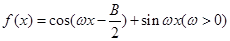 ,且
,且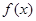 的最小正周期为
的最小正周期为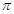 ,求
,求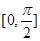 上的最大值和最小值.
上的最大值和最小值.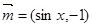 ,向量
,向量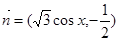 ,函数
,函数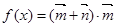 .
.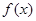 的最小正周期
的最小正周期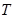 ;
;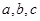 分别为
分别为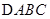 内角
内角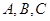 的对边,
的对边,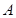 为锐角,
为锐角,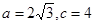 ,且
,且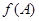 恰是
恰是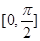 上的最大值,求
上的最大值,求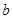 .
.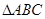 中,角
中,角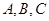 的对边分别为
的对边分别为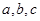 .已知
.已知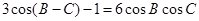 .
.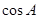 ;
;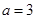 ,
,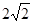 ,且
,且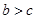 ,求
,求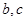 .
.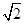 ],则b-a的取值范围是________.
],则b-a的取值范围是________.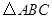 的内角
的内角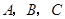 所对的边长分别为
所对的边长分别为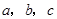 ,且
,且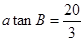 ,
,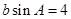 ,则
,则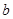 的最小值是( )
的最小值是( )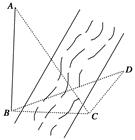
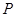 是
是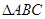 所在平面上的一点,满足
所在平面上的一点,满足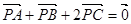 ,若
,若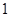 ,则
,则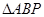 的面积为______________.
的面积为______________.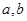 为单位向量,若向量c满足
为单位向量,若向量c满足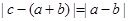 ,则
,则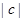 的最大值是( )
的最大值是( )