题目内容
给出下列六个命题:①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x)=0,则函数y=f(x)在x=x处取得极值;
③若m≥-1,则函数y=
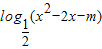 的值域为R;
的值域为R;④“a=1”是“函数
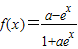 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.⑤函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称;
⑥满足条件AC=
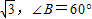 ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.其中正确命题的个数是 .
【答案】分析:根据函数零点的判定定理可得①正确. 通过举反例可得②不正确.
根据对数的真数可取遍所有的正实数,可得此对数函数的值域为R,故③正确.
根据a=1时,函数在定义域上是奇函数,再根据函数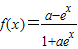 在定义域上是奇函数时,a=±1,可得④正确.
在定义域上是奇函数时,a=±1,可得④正确.
由函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称,可得⑤正确.
由AC=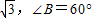 ,AB=1,利用正弦定理及由大边对大角可得△ABC是一个唯一的直角三角形,故⑥不正确.
,AB=1,利用正弦定理及由大边对大角可得△ABC是一个唯一的直角三角形,故⑥不正确.
解答:解:对于函数f(x)=lnx-2+x,在区间(1,e)上单调递增,f(1)=-1,f(e)=e-1>0,根据函数零点的判定定理
可得,在区间(1,e)上存在零点,故①正确.
②不正确,如当f(x)=x3时,显然满足f′(0)=0,但y=f(x)=x3 在x=0处没有极值.
③当 m≥-1,函数y=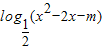 的真数为 x2-2x-m,判别式△=4+4m≥0,故真数可取遍所有的正实数,
的真数为 x2-2x-m,判别式△=4+4m≥0,故真数可取遍所有的正实数,
故函数y=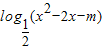 的值域为R,故③正确.
的值域为R,故③正确.
④由a=1可得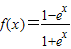 ,定义域为R,关于原点对称,
,定义域为R,关于原点对称,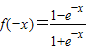 =
=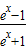 =-f(x),故函数在
=-f(x),故函数在
定义域上是奇函数,故充分性成立.
若函数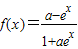 在定义域上是奇函数,则有f(0)=0,或f(0)不存在,∴a=1,或a=-1,故不能推出a=1.
在定义域上是奇函数,则有f(0)=0,或f(0)不存在,∴a=1,或a=-1,故不能推出a=1.
故必要性不成立,故④正确.
⑤在函数y=f(1+x)的图象上任意取一点(a,f(1+a)),则点(a,f(1+a))关于y轴的对称点为
(-a,f(1-a)),故函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称,故⑤正确.
⑥△ABC中,由AC=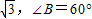 ,AB=1,利用正弦定理求得sinC=
,AB=1,利用正弦定理求得sinC= ,再由大边对大角可得C=30°,∴B=90°,
,再由大边对大角可得C=30°,∴B=90°,
△ABC是一个唯一的直角三角形,故⑥不正确.
故答案为 ①③④⑤.
点评:本题主要考查命题的真假的判断,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于基础题.
根据对数的真数可取遍所有的正实数,可得此对数函数的值域为R,故③正确.
根据a=1时,函数在定义域上是奇函数,再根据函数
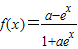 在定义域上是奇函数时,a=±1,可得④正确.
在定义域上是奇函数时,a=±1,可得④正确.由函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称,可得⑤正确.
由AC=
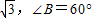 ,AB=1,利用正弦定理及由大边对大角可得△ABC是一个唯一的直角三角形,故⑥不正确.
,AB=1,利用正弦定理及由大边对大角可得△ABC是一个唯一的直角三角形,故⑥不正确.解答:解:对于函数f(x)=lnx-2+x,在区间(1,e)上单调递增,f(1)=-1,f(e)=e-1>0,根据函数零点的判定定理
可得,在区间(1,e)上存在零点,故①正确.
②不正确,如当f(x)=x3时,显然满足f′(0)=0,但y=f(x)=x3 在x=0处没有极值.
③当 m≥-1,函数y=
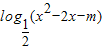 的真数为 x2-2x-m,判别式△=4+4m≥0,故真数可取遍所有的正实数,
的真数为 x2-2x-m,判别式△=4+4m≥0,故真数可取遍所有的正实数,故函数y=
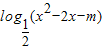 的值域为R,故③正确.
的值域为R,故③正确.④由a=1可得
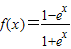 ,定义域为R,关于原点对称,
,定义域为R,关于原点对称,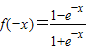 =
=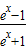 =-f(x),故函数在
=-f(x),故函数在定义域上是奇函数,故充分性成立.
若函数
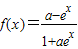 在定义域上是奇函数,则有f(0)=0,或f(0)不存在,∴a=1,或a=-1,故不能推出a=1.
在定义域上是奇函数,则有f(0)=0,或f(0)不存在,∴a=1,或a=-1,故不能推出a=1.故必要性不成立,故④正确.
⑤在函数y=f(1+x)的图象上任意取一点(a,f(1+a)),则点(a,f(1+a))关于y轴的对称点为
(-a,f(1-a)),故函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称,故⑤正确.
⑥△ABC中,由AC=
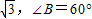 ,AB=1,利用正弦定理求得sinC=
,AB=1,利用正弦定理求得sinC= ,再由大边对大角可得C=30°,∴B=90°,
,再由大边对大角可得C=30°,∴B=90°,△ABC是一个唯一的直角三角形,故⑥不正确.
故答案为 ①③④⑤.
点评:本题主要考查命题的真假的判断,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于基础题.

练习册系列答案
相关题目
 ,给出下列六个命题:(1)若
,给出下列六个命题:(1)若 是
是 ,则
,则 的
的 对称,则
对称,则 与函数
与函数 的
的 ,则
,则 ,则
,则 的图像仅通过平移变
的图像仅通过平移变