题目内容
给出下列六个命题,其中正确的命题是①存在α满足sinα+cosα=
| 3 |
| 2 |
②y=sin(
| 5 |
| 2 |
③x=
| π |
| 8 |
| 5π |
| 4 |
④y=esin2x是以π为周期的(0,
| π |
| 2 |
⑤若α、β是第一象限角,且α>β,则tanα>tanβ;
⑥函数y=3sin(2x+
| π |
| 3 |
| π |
| 3 |
分析:本题利用直接法对六个命题进行逐一进行判定即可.
解答:解:①sinα+cosα=
sin(α+
)∈[-
,
],∴sinα+cosα≠
,故不正确.
②y=sin(
-2x)=sin(
-2x)=cos2x,是偶函数,故正确.
③对y=sin(2x+
),由2x+
=
+kπ,得x=-
+
,(k∈Z)是对称轴方程.取k=1得x=
,故正确.
④y=sin2x在(0,
)上不是增函数,∴y=esin2x在(0,
)上也不是增函数,故错误.
⑤y=tanx在第一象限不是增函数.∴α>β,不一定有tanα>tanβ,故错误.
⑥y=3sin(2x+
)=3sin2(x+
),可由y=3sin2x的图象向左平移
个单位得到,故错误.
故选②③
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| 3 |
| 2 |
②y=sin(
| 5π |
| 2 |
| π |
| 2 |
③对y=sin(2x+
| 5π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| kπ |
| 2 |
| π |
| 8 |
④y=sin2x在(0,
| π |
| 2 |
| π |
| 2 |
⑤y=tanx在第一象限不是增函数.∴α>β,不一定有tanα>tanβ,故错误.
⑥y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
故选②③
点评:本题主要考查了正弦函数的奇偶性、单调性、对称性,以及函数y=Asin(ωx+φ)的图象变换,属于基础题.

练习册系列答案
相关题目
 ;
; π-2x)是偶函数;
π-2x)是偶函数;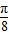 是y=sin(2x+
是y=sin(2x+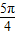 )的一条对称轴;
)的一条对称轴;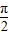 )上的增函数;
)上的增函数;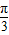 )的图象可由y=3sin2x的图象向左平移
)的图象可由y=3sin2x的图象向左平移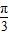 个单位得到.
个单位得到.