题目内容
已知数列{an}中a1=2,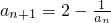 ,数列{bn}中
,数列{bn}中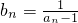 ,其中 n∈N*.
,其中 n∈N*.
(Ⅰ)求证:数列{bn}是等差数列;
(Ⅱ)设Sn是数列{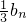 }的前n项和,求
}的前n项和,求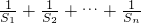 ;
;
(Ⅲ)设Tn是数列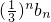 的前n项和,求证:
的前n项和,求证: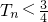 .
.
解:(Ⅰ)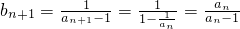 ,而
,而 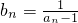 ,
,
∴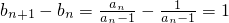 .n∈N*
.n∈N*
∴{bn}是首项为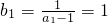 ,公差为1的等差数列.(5分)
,公差为1的等差数列.(5分)
(Ⅱ)由(Ⅰ)可知bn=n,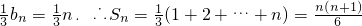 ,
,
于是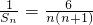 =
=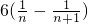 ,
,
故有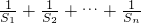 =
=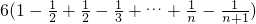
=6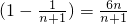 .(9分)
.(9分)
(Ⅲ)证明:由(Ⅰ)可知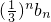 =
=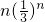 ,
,
则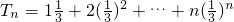 .∴
.∴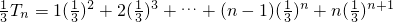 .
.
则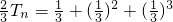 +…+
+…+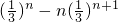 =
=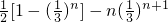 ,
,
∴Tn=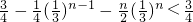 . (14分)
. (14分)
分析:(Ⅰ)由条件可得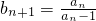 ,再由
,再由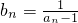 ,从而得到
,从而得到 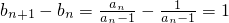 ,由此证得结论
,由此证得结论
(Ⅱ)由(Ⅰ)可知bn=n,于是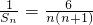 =
=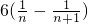 ,用裂项法求出
,用裂项法求出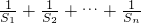 的值.
的值.
(Ⅲ)由(Ⅰ)可知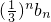 =
=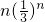 ,求出Tn的解析式,可得
,求出Tn的解析式,可得 Tn 的解析式,用错位相减法求出Tn的解析式,
Tn 的解析式,用错位相减法求出Tn的解析式,
从而可得要证的不等式成立.
点评:本题主要考查等差关系的确定,等比数列的前n项和公式的应用,用裂项法、错位相减法对数列求和,数列与不等式的综合应用,属于中档题.
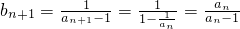 ,而
,而 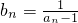 ,
,∴
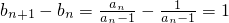 .n∈N*
.n∈N*∴{bn}是首项为
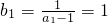 ,公差为1的等差数列.(5分)
,公差为1的等差数列.(5分)(Ⅱ)由(Ⅰ)可知bn=n,
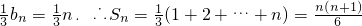 ,
,于是
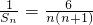 =
=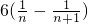 ,
,故有
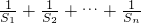 =
=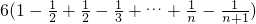
=6
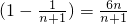 .(9分)
.(9分)(Ⅲ)证明:由(Ⅰ)可知
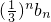 =
=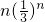 ,
,则
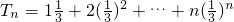 .∴
.∴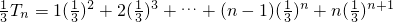 .
.则
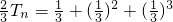 +…+
+…+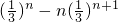 =
=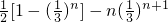 ,
,∴Tn=
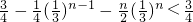 . (14分)
. (14分)分析:(Ⅰ)由条件可得
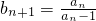 ,再由
,再由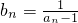 ,从而得到
,从而得到 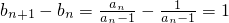 ,由此证得结论
,由此证得结论(Ⅱ)由(Ⅰ)可知bn=n,于是
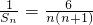 =
=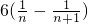 ,用裂项法求出
,用裂项法求出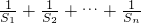 的值.
的值.(Ⅲ)由(Ⅰ)可知
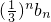 =
=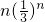 ,求出Tn的解析式,可得
,求出Tn的解析式,可得 Tn 的解析式,用错位相减法求出Tn的解析式,
Tn 的解析式,用错位相减法求出Tn的解析式,从而可得要证的不等式成立.
点评:本题主要考查等差关系的确定,等比数列的前n项和公式的应用,用裂项法、错位相减法对数列求和,数列与不等式的综合应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目