题目内容
6.已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y=$\frac{1}{2}$x2-x+$\frac{5}{2}$,0≤x≤3}.(1)若A∩B=∅,求a的取值范围;
(2)当a取使不等式x2+1≥ax恒成立的a的最小值时,求(∁RA)∩B.
分析 (1)先解出集合中的一元二次不等式,然后根据A∩B=空集,说明集合A,B没有共同的元素,从而求出实数a的范围;
(2)由条件判断a=-2,求出CRA,即可求得(CRA)∩B.
解答 解:(1)∵y=$\frac{1}{2}$x2-x+$\frac{5}{2}$=$\frac{1}{2}$(x-1)2+2,
∴y=$\frac{1}{2}$x2-x+$\frac{5}{2}$在[0,1]递减,在[1,3]上递增,
当x=1时,有最小值,即为2,当x=3时,有最大值,即为4,
∴2≤y≤4,
∴B=[2,4],
∵A={y|y2-(a2+a+1)y+a(a2+1)>0}═{y|(y-a)[y-(a2+1)]>0},又a2+1>a
∴A={y>a2+1或y<a},
∵A∩B=∅,
∴a2+1≥4或a≤2,
∴$\sqrt{3}$≤a≤2或a≤-$\sqrt{3}$,
(2)使不等式x2+1≥ax恒成立时,即x2+1-ax≥0,由判别式△=a2-4≤0,解得-2≤a≤2,
故当a取使不等式x2+1≥ax恒成立的最小值时,a=-2.
由(1)可得CRA={y|a≤y≤a2+1 }={y|-2≤y≤5},B={y|2≤y≤4}.
(CRA)∩B=B=[2,4].
点评 本题主要考查两个集合的补集、交集、并集的定义和运算,二次函数的性质,属于基础题

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 命题“若x<1,则-≤x≤1”的逆否命题是“若x≥1,则x<-1或x≥1” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 已知命题p:?x∈R,lnx<lgx;命题q:?x0∈R,x03=1-x02,则“(¬p)∨(¬q)为真命题”. |
14.如图可表示函数y=f(x)图象的是( )
| A. | 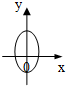 | B. | 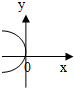 | C. | 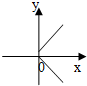 | D. | 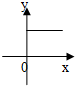 |
11.已知点An(n,an)(n∈N*)都在函数f(x)=logax(a>0且a≠1)的图象上,则a2+a10与2a6的大小关系为( )
| A. | a2+a10>2a6 | B. | a2+a10<2a6 | ||
| C. | a2+a10=2a6 | D. | a2+a10与2a6的大小与a有关 |
18. 在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AE}$等于( )
在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AE}$等于( )
 在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AE}$等于( )
在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AE}$等于( )| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{3}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
16.在一段线路中并联着两个独立自动控制的开关,只要其中一个开关能够闭合,线路就可以正常工作.设这两个开关能够闭合的概率分别为0.5和0.7,则线路能够正常工作的概率是( )
| A. | 0.35 | B. | 0.65 | C. | 0.85 | D. | $\frac{5}{7}$ |