题目内容
 给出下列命题:
给出下列命题:①已知函数f(x)=(
| 1 |
| 2x-1 |
②若函数f(x)=lg(x2+ax-a)的值域是R,则a∈(-4,0);
③关于x的方程(
| 1 |
| 2 |
④如图,三棱柱ABC-A1B1C1中,E、F分别是AB,AC的中点,平面EB1C1F将三棱柱分成几何体AEF-AB1C1和B1C1-EFCB两部分,其体积分别为V1,V2,则V1:V2=7:5.
其中正确命题的序号是
①③④
①③④
.分析:①、假设为真,则loga1000=lglg2,若存在大于0且不为1的实数a,则命题为真,否则为假;
②、由于函数值域是R,则真数取遍(0,+∞)的所有数,进而得到a的范围;
③、由题意知,0<lga<1,解出不等式即可;
④、依据棱柱与棱台的体积公式,求出体积,进而得到结论.
②、由于函数值域是R,则真数取遍(0,+∞)的所有数,进而得到a的范围;
③、由题意知,0<lga<1,解出不等式即可;
④、依据棱柱与棱台的体积公式,求出体积,进而得到结论.
解答:解:①、由题意知,函数f(x)=(
)•x2-sinx+a(a为常数)既不是奇函数也不是偶函数,
若命题为真命题,则loga1000=lglg2,
由于lglg2∈(-∞,0),则存在实数a∈(0,1)使上述方程成立,故①正确;
②、由于函数值域是R,则真数t=x2+ax-a需取遍(0,+∞)的所有数,
则△=a2+4a≥0,解得 a≤-4或a≥0,故②错;
③、由于x的方程(
)x=lga有非负实数根,所以x>0,则(
)x∈(0,1)
得到0<lga<1,解得1<a<10,故③正确;
④、若设三棱柱ABC-A1B1C1的底面积为S,高为h,则其体积为Sh,
由题意可得三棱台AEF-AB1C1的上下两底面的面积分别是S与
S,高为h,
得到此三棱台的体积是
Sh,则另一部分的体积是
Sh,故④正确.
故答案为 ①③④.
| 1 |
| 2x-1 |
若命题为真命题,则loga1000=lglg2,
由于lglg2∈(-∞,0),则存在实数a∈(0,1)使上述方程成立,故①正确;
②、由于函数值域是R,则真数t=x2+ax-a需取遍(0,+∞)的所有数,
则△=a2+4a≥0,解得 a≤-4或a≥0,故②错;
③、由于x的方程(
| 1 |
| 2 |
| 1 |
| 2 |
得到0<lga<1,解得1<a<10,故③正确;
④、若设三棱柱ABC-A1B1C1的底面积为S,高为h,则其体积为Sh,
由题意可得三棱台AEF-AB1C1的上下两底面的面积分别是S与
| 1 |
| 4 |
得到此三棱台的体积是
| 7 |
| 12 |
| 5 |
| 12 |
故答案为 ①③④.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数和对数函数的一些性质,我们可以根据三角函数,对数函数的性质对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.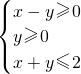 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.