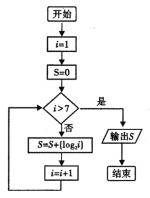
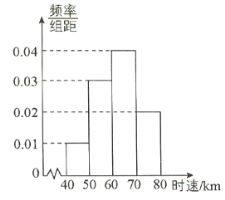
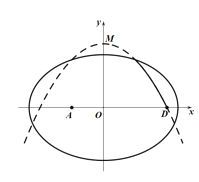
题目内容
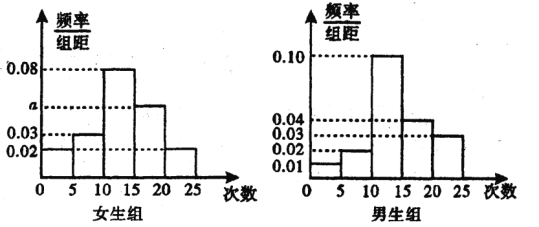
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了 40 名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(1)求![]() 的值;
的值;
(2)求抽取的40名学生中月上网次数不少于15次的人数;
(3)再从月上网次数不少于20 次的学生中随机抽取2人,求至少抽到1名女生的概率.
【答案】(1)![]() ;(2)
;(2)![]() 人;(3)
人;(3)![]() .
.
【解析】
(1)根据频率分布直方图计算a的值即可;
(2)根据频率直方图求出女生、男生月上网次数不少于15次的频率,计算对应的频数,再求和;
(3)利用列举法求基本事件数,计算对应的概率值即可.
解析:(1)由![]() ,得
,得![]() .
.
(2)在所抽取的女生中,月上网次数不少于15次的学生频率为![]() ,
,
∴在所抽取的女生中,月上网次数不少于15次的学生有![]() 人.
人.
在所抽取的男生中,月上网次数不少于15次的学生频率为![]() ,
,
∴在所抽取的男生中,月上网次数不少于15次的学生有![]() 人.
人.
故抽取的40名学生中月上网次数不少于15次的人数有![]() 人.
人.
(3)记“再从月上网次数不少于20次的学生中随机抽取2人,至少抽到1名女生”为事件![]() ,
,
在抽取的女生中,月上网次数不少于20次的学生频率为![]() ,人数为
,人数为![]() .
.
在抽取的男生中,月上网次数不少于20次的学生频率为![]() ,
,
人数为![]() . 记两名女生为
. 记两名女生为![]() ,
,![]() ,三名男生为
,三名男生为![]() ,
,![]() ,
,![]() ,
,
则在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人,所有可能有 10种:
即![]() ,
,![]() ,
,![]() ,,
,,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
而事件![]() 包含的结果有 7 种:
包含的结果有 7 种:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.

【题目】电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 | 0.4 | 0.2 | 0.15 | 0.25 | 0.2 | 0.1 |
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取1部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)