题目内容
如图所示,A是△BCD所在平面外一点,∠ABD=∠ACD= ,AB=AC,E是BC的中点.
,AB=AC,E是BC的中点.

(1)求证:AD⊥BC;
(2)试判断△ADE的形状,并证明你的结论.
答案:
解析:
解析:
|
(1)∵AB=AC,E是BC中点 BC⊥AE 在△ABD,△ACD中,∠ABD=∠ACD= ∴△ABD≌△ACD,于是BD=DC ∵E中BC的中点,∴BC⊥ED 由BC⊥AE,AE∩ED=E,∴BC⊥平面AED ∵AD (2)∵AE2=AB2- ∴AE2+DE2-AD2= ∴cos∠AED= ∴∠AED是钝角,故△AED是钝角三角形. |

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
如图所示,D是△ABC的边AB的中点,|
|=6,|
|=4,向量
,
的夹角为120°,则
•
等于( )

| BC |
| AC |
| AC |
| CB |
| CD |
| CB |

A、18+12
| ||
| B、24 | ||
| C、12 | ||
D、18-12
|
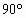 ,AB=AC,AD为公共边
,AB=AC,AD为公共边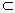 平面ADE,∴AD⊥BC
平面ADE,∴AD⊥BC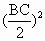 ,DE2=DC2-
,DE2=DC2-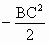
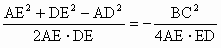 <0
<0 如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.
如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8. 如图所示,ABCD是一平面图形的水平放置的斜二侧直观图.在斜二侧直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行.若AB=6,AD=2,则这个平面图形的实际面积为( )
如图所示,ABCD是一平面图形的水平放置的斜二侧直观图.在斜二侧直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行.若AB=6,AD=2,则这个平面图形的实际面积为( ) 如图所示,D是△ABC的边BC上的中点,若
如图所示,D是△ABC的边BC上的中点,若