题目内容

如图所示，D是△ABC的边BC上的中点，若
AB
=
a
，
AC
=
b
，则向量
AD
=
1
2
a
+
1
2
b
1
2
a
+
1
2
b
．（用
a
，
b
表示）
分析：直接利用向量的加法的平行四边形法则，求出结果即可．
解答：解：因为D是△ABC的边BC上的中点，若
AB
=
a
，
AC
=
b
，
所以向量
AD
=
1
2
(
AC
+
AB
)=
1
2
a
+
1
2
b
．
故答案为：
1
2
a
+
1
2
b
．
点评：本题考查向量的四边形法则的应用，考查计算能力．
练习册系列答案
相关题目
如图所示，D是△ABC的边AB的中点，|
BC
|=6，|
AC
|=4，向量
AC
，
CB
的夹角为120°，则
CD
•
CB
等于（　　）
精英家教网
A、18+12
3
B、24
C、12
D、18-12
3
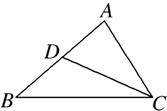精英家教网如图所示，D是△ABC的边AB的中点，则向量
CD
=（　　）
A、-
BC
+
1
2
BA
B、-
BC
-
1
2
BA
C、
BC
-
1
2
BA
D、
BC
+
1
2
BA
如图所示，D是△ABC的边AB上的中点，记
BC
=
a
，
BA
=
c
，则向量
CD
=（　　）
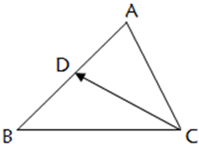精英家教网如图所示，D是△ABC的边AB的中点，|
BC
|=6，|
AC
|=4，向量
AC
，
CB
的夹角为120°，则
CD
•
CB
等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网