题目内容
如图所示，D是△ABC的边AB的中点，|
|=6，|
|=4，向量
，
的夹角为120°，则
•
等于（ ）
| BC |
| AC |
| AC |
| CB |
| CD |
| CB |
A、18+12
| ||
| B、24 | ||
| C、12 | ||
D、18-12
|
分析：考查向量和三角形的知识．基础题．由D为AB中点，则
=
(
+
)，将未知向量用已知向量表示后，代入向量内积公式，易得结果．
| CD |
| 1 |
| 2 |
| CA |
| CB |
解答：解：∵D为AB中点，
∴
=
(
+
)，
∵向量
，
的夹角为120°
∴＜
，
＞=60°
∴
•
=
(
+
)•
=
(
•
+
2)
=6+18=24
故选B．
∴
| CD |
| 1 |
| 2 |
| CA |
| CB |
∵向量
| AC |
| CB |
∴＜
| CA |
| CB |
∴
| CD |
| CB |
| 1 |
| 2 |
| CA |
| CB |
| CB |
=
| 1 |
| 2 |
| CA |
| CB |
| CB |
=6+18=24
故选B．
点评：本题考查的主要知识是平面向量的数量积．即：
•
=|
|•|
•cosθ
①当＜
，
＞为锐角或零角时，cosθ＞0时，
•
＞0
特别的，当＜
，
＞=0，即两向量同向时，即cosθ=1时，
•
有最大值：|
|•|
|．
②当＜
，
＞为直角时，cosθ=0时，
•
=0
③当＜
，
＞为钝角或夹角时，cosθ＜0时，
•
＜0
特别的，当＜
，
＞=π，即两向量反向时，cosθ=-1时，
•
有最小值：-|
|•|
|．
| a |
| b |
| a |
| b| |
①当＜
| a |
| b |
| a |
| b |
特别的，当＜
| a |
| b |
| a |
| b |
| a |
| b |
②当＜
| a |
| b |
| a |
| b |
③当＜
| a |
| b |
| a |
| b |
特别的，当＜
| a |
| b |
| a |
| b |
| a |
| b |
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
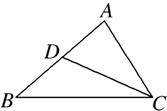如图所示，D是△ABC的边AB的中点，则向量| CD |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
如图所示，D是△ABC的边BC上的中点，若
如图所示，D是△ABC的边AB上的中点，记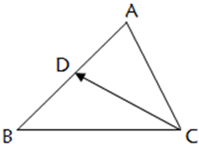
如图所示，D是△ABC的边AB的中点，