题目内容
如图是总体的一个样本频率分布直方图,且在区间[15,18)内的频数为8.
(1)求样本容量;
(2)若在[12,15)内的小矩形的面积为0.06,
①求样本在[12,15)内的频数;
②求样本在[18,33)内的频率。
(1)50;(2)3;0.78.
解析试题分析:(1)根据在[15,18)内频数为8.做出在这一个范围中频率是小正方形的面积是 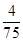 ×3,知道频率和频数做出样本容量.
×3,知道频率和频数做出样本容量.
(2)①在[12,15)内的小矩形面积为0.06,即这组数据的频率是0.06,用频率乘以样本容量作出在[12,15)内的频数,得到结果.
②根据在[15,18)内频数为8,在[12,15)内的频数是3,而样本容量是50,剩下的部分是要求的频数,只要样本容量减去前两组的频数,得到样本在[18,33)内的频数39,所以样本在[18,33)内的频率为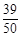 =0.78.
=0.78.
试题解析:(1)由图可知在[15,18)内的频率为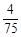 ×3=
×3= 又频数为8
又频数为8
∴样本容量n=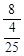 =50 4分
=50 4分
(2)∵样本在[12,15)内的频率为0.06
①∴样本在[12,15)内的频数为50×0.06=3 8分
②∵样本在[18,33)内的频数为50―3―8=39
∴样本在[18,33)内的频率为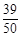 =0.78 12分
=0.78 12分
考点:频率分布直方图.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  | 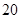 |  |
| 第五组 |  |  |  |
| 合计 |  |  | |
 、
、 、
、 的值;
的值;(2)若从第三、四、五组中用分层抽样方法抽取
 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率 从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |  |  |  |  |
| 频数(个) | 5 | 10 | 20 | 15 |
 的频率;
的频率;(2)用分层抽样的方法从重量在
 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?(3)在(2)中抽出的4个苹果中,任取2个,求重量在
 和
和 中各有1个的概率.
中各有1个的概率. 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
| 组别 | 频数 | 频率 |
| 145.5~149.5 | 8 | 0.16 |
| 149.5~153.5 | 6 | 0.12 |
| 153.5~157.5 | 14 | 0.28 |
| 157.5~161.5 | 10 | 0.20 |
| 161.5~165.5 | 8 | 0.16 |
| 165.5~169.5 |  |  |
| 合计 |  |  |
 所对应的数值;
所对应的数值;(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5
 范围内有多少人?
范围内有多少人? 为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
| 年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
研究性学习小组为了解某生活小区居民用水量 (吨)与气温
(吨)与气温 (℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
(℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
| 日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
气温 (℃) (℃) | 18 | 15 | 11 | 9 | -3 |
用水量 (吨) (吨) | 57 | 46 | 36 | 37 | 24 |
(2)由表中数据求得线性回归方程
 中的
中的 ,试求出
,试求出 的值,并预测当地气温为5℃时,该生活小区的用水量.
的值,并预测当地气温为5℃时,该生活小区的用水量. 
 ;
; =40
=40