题目内容
给出下列三个命题:①若直线l过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为2;
②双曲线
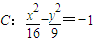 的离心率为
的离心率为 ;
;③若
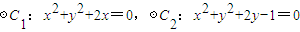 ,则这两圆恰有2条公切线;
,则这两圆恰有2条公切线;④若直线l1:a2x-y+6=0与直线l2:4x-(a-3)+9-0互相垂直,则a=-1.
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
【答案】分析:①利用|AB|的最小值为抛物线的通径2p,进行判断.
②先将双曲线方程化成标准形式,再利用其几何性质求出离心率即可进行判断.
③求出两个圆的圆心和半径,再求出圆心距,由两圆的圆心距等于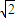 ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论.
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论.
④由直线垂直的等价条件求出两直线垂直时a的值,再判断其是否成立.
解答:解:①∵过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为抛物线的通径2p,由抛物线y=2x2
的方程即x2= y 知,p=
y 知,p= ,2p=
,2p= ,则|AB|的最小值为
,则|AB|的最小值为  ,故①不正确.
,故①不正确.
②双曲线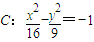 即
即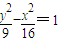 ,
,
a=3,b=4,c=5,∴它的离心率为 ;正确.
;正确.
③∵⊙C1:x2+y2+2x=0,即 (x+1)2+y2=1,表示圆心为(-1,0),半径等于1的圆.
⊙C2:x2+y2+2y-1=0 即,x2+(y+1)2=2,表示圆心为(0,-1),半径等于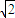 的圆.
的圆.
两圆的圆心距等于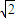 ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线
由2条,故③正确.
④当直线a2x-y+6=0与4x-(a-3)y+9=0互相垂直时,则有4a2+(a-3)=0,解得a=-1或 ,故错.
,故错.
故答案为:②③.
点评:本题考查直线、抛物线、双曲线、圆的性质,两圆的位置关系,掌握圆锥曲线的性质是解题的关键.
②先将双曲线方程化成标准形式,再利用其几何性质求出离心率即可进行判断.
③求出两个圆的圆心和半径,再求出圆心距,由两圆的圆心距等于
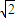 ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论.
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论.④由直线垂直的等价条件求出两直线垂直时a的值,再判断其是否成立.
解答:解:①∵过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为抛物线的通径2p,由抛物线y=2x2
的方程即x2=
 y 知,p=
y 知,p= ,2p=
,2p= ,则|AB|的最小值为
,则|AB|的最小值为  ,故①不正确.
,故①不正确.②双曲线
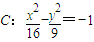 即
即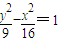 ,
,a=3,b=4,c=5,∴它的离心率为
 ;正确.
;正确.③∵⊙C1:x2+y2+2x=0,即 (x+1)2+y2=1,表示圆心为(-1,0),半径等于1的圆.
⊙C2:x2+y2+2y-1=0 即,x2+(y+1)2=2,表示圆心为(0,-1),半径等于
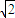 的圆.
的圆.两圆的圆心距等于
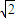 ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线由2条,故③正确.
④当直线a2x-y+6=0与4x-(a-3)y+9=0互相垂直时,则有4a2+(a-3)=0,解得a=-1或
 ,故错.
,故错.故答案为:②③.
点评:本题考查直线、抛物线、双曲线、圆的性质,两圆的位置关系,掌握圆锥曲线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目