题目内容
已知随机变量ξ的分布列为P（ξ=k）=
，k=1、2、3、4，则P（2＜ξ≤4）等于
．
| m |
| 2k |
| 1 |
| 5 |
| 1 |
| 5 |
分析：根据已知条件以及概率分布列的性质可得
+
+
+
=
=1，求得m的值，再由P（2＜ξ≤4）=P（ξ=3）+P（ξ=4）=
+
，运算求得结果．
| m |
| 2 |
| m |
| 22 |
| m |
| 23 |
| m |
| 24 |
| 15m |
| 16 |
| m |
| 8 |
| m |
| 16 |
解答：解：由随机变量ξ的分布列为P（ξ=k）=
，k=1、2、3、4，以及概率分布列的性质可得
+
+
+
=
=1，∴m=
．
故P（2＜ξ≤4）=P（ξ=3）+P（ξ=4）=
+
=
，
故答案为
．
| m |
| 2k |
| m |
| 2 |
| m |
| 22 |
| m |
| 23 |
| m |
| 24 |
| 15m |
| 16 |
| 16 |
| 15 |
故P（2＜ξ≤4）=P（ξ=3）+P（ξ=4）=
| m |
| 8 |
| m |
| 16 |
| 1 |
| 5 |
故答案为
| 1 |
| 5 |
点评：本题主要考查随机变量ξ的分布列的性质应用，属于中档题．
练习册系列答案
相关题目
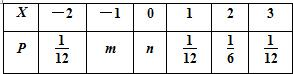已知随机变量X的分布列如图：其中m，n∈[0，1），且E（X）=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|