Question

【题目】如图，正三棱柱 中， 是 的中点.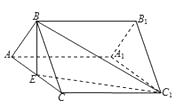

（1）求证：平面 ；
（2）若 ，求点 到平面 的距离.

Answer 1

【答案】
（1）证明：∵ 是正三棱柱，

∴ 平面 ，又 平面 ，∴ .∵ 是正三角形， 是 中点，

∴ ，又 ， 平面 ， 平面 ，

∴ 平面 ，

∵ 平面 ，

∴平面 ⊥平面

（2）解 : 正三棱柱 中， ，因为 是 中点，

∴ ，

∴ .

在直角 中， ，

∵ 平面 ，

平面 ，∴ ，

∴ .

设点 到面 的距离为 ，

∵ ，∴ ，

∴ .

【解析】(1)由题意结合正三棱柱的性质可知A A1 ⊥ 平面 A B C进而得到 B E ⊥ A A1，由 Δ A B C 是正三角形 E 是 A C 中点，可得B E ⊥ A C 再由线面垂直的判定定理可得出B E ⊥ 平面 A C C1 A1，进而得到面面垂直。(2)根据题意可知点A到平面BEC1的距离即点C到平面BEC1的距离，过点C作出，则可证CH垂直于平面BEC1，故CH为点 C到平面 B E C1的距离即为点 A 到平面 B E C1的距离.