题目内容

在计算“1×2+2×3+…+n（n+1）”时，有如下方法：
先改写第k项：k（k+1）= $数学公式$ [k（k+1）（k+2）-（k-1）k（K+1）]，
由此得：1×2= $数学公式$ （1×2×3-0×1×2），
2×3= $数学公式$ （2×3×4-1×2×3），…，
n（n+1）= $数学公式$ [n（n+1）（n+2）-（n-1）n（n+1）]，
相加得：1×2+2×3+…+n（n+1）= $数学公式$ （n+1）（n+2）．
类比上述方法，请你计算“1×3+2×4+…+n（n+2）”，其结果写成关于n的一次因式的积的形式为：________．

$\text{[math]}$ n（n+1）（2n+7）
分析：类比，先改写第k项k（k+2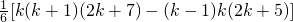）= $\text{[math]}$ ，再累加，即可求得结论．
解答：由题意，k（k+2）= $\text{[math]}$
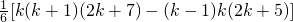
由此得：1×3= $\text{[math]}$ （1×2×9-0×1×7）），
2×3= $\text{[math]}$ （2×3×11-1×2×9），
…，
n（n+2）= $\text{[math]}$
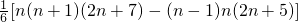
相加得：1×3+2×4+…+n（n+2）= $\text{[math]}$ n（n+1）（2n+7）
故答案为： $\text{[math]}$ n（n+1）（2n+7）
点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．

练习册系列答案

名师面对面同步课堂系列答案

精英口算卡系列答案

小学生每日10分钟系列答案

天利38套高中名校期中期末联考测试卷系列答案

口算题应用题天天练神机妙算系列答案

应用题点拨系列答案

培优新方法系列答案

状元及第系列答案

名师教你学数学系列答案

同步奥数系列答案

相关题目

在计算“1×2+2×3+…+n（n+1）”时，某同学学到了如下一种方法：先改写第k项：k（k+1）=

[k（k+1）（k+2）-（k-1）k（k+1）]由此得
1×2=

（1×2×3-0×1×2），
2×3=

（2×3×4-1×2×3）
…
n（n+1）=

[n（n+1）（n+2）-（n-1）n（n+1）]
相加，得1×2×3+…+n（n+1）=

n（n+1）（n+2）
类比上述方法，请你计算“1×2×3+2×3×4+…+n（n+1）（n+2）”，

其结果为

在计算“1×2+2×3+…+n（n+1）”时，有如下方法：
先改写第k项：k（k+1）=

[k（k+1）（k+2）-（k-1）k（K+1）]，
由此得：1×2=

（1×2×3-0×1×2），
2×3=

（2×3×4-1×2×3），…，
n（n+1）=

[n（n+1）（n+2）-（n-1）n（n+1）]，
相加得：1×2+2×3+…+n（n+1）=

n（n+1）（n+2）．
类比上述方法，请你计算“1×3+2×4+…+n（n+2）”，其结果写成关于n的一次因式的积的形式为：

n（n+1）（2n+7）

n（n+1）（2n+7）

在计算“1×2+2×3+…n（n+1）”时，先改写第k项：
k（k+1）=

[k（k+1）（k+2）-（k-1）k（k+1）]，由此得1×2=

（1×2×3-0×1×2），2×3=

（2×3×4-1×2×3），．．
n（n+1）=

[n（n+1）（n+2）-（n-1）n（n+1）]，相加，得1×2+2×3+…+n（n+1）=

n(n+1)(n+2)
（1）类比上述方法，请你计算“1×2×3+2×3×4+…+n（n+1）（n+2）”的结果；
（2）试用数学归纳法证明你得到的等式．

在计算“1×2＋2×3＋…＋n(n＋1)”时，某同学学到了如下一种方法：先改写第k项：k(k＋1)＝[k(k＋1)(x＋2)－(k－1)k(k＋1)]，由此得

1×2＝(1×2×3－0×1×2)

2×3＝(2×3×4－1×2×3)

…

n(n＋1)＝[n(n＋1)(n＋2)－(n－1)n(n＋1)]

相加，得

1×2＋2×3＋…＋n(n＋1)＝n(n＋1)(n＋2)

类比上述方法，请你计算“1×2×3＋2×3×4＋…＋n(n＋1)(n＋2)”，其结果为________．