题目内容
已知 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.
(1)若 ,求
,求 的面积;
的面积;
(2)若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.(1)若
 ,求
,求 的面积;
的面积;(2)若关于
 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.(1)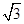 ;(2)
;(2)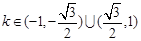
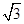 ;(2)
;(2)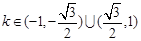
试题分析:(1)由数量积的坐标运算,将
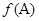 表示为
表示为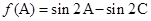 ,然后利用
,然后利用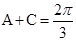 ,将其转换为关于
,将其转换为关于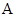 的一元函数,并将其变形为
的一元函数,并将其变形为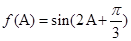 ,计算
,计算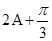 的范围,又
的范围,又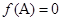 ,从而可求出
,从而可求出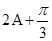 的值,进而确定
的值,进而确定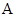 ,从而可求
,从而可求 的面积;(2) 方程
的面积;(2) 方程 有两个不同的实数解,即函数
有两个不同的实数解,即函数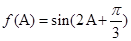 (
(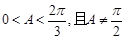 )的图象和直线
)的图象和直线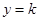 有两个不同的交点,为了便于画图象,可设
有两个不同的交点,为了便于画图象,可设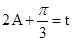 ,这样只需画
,这样只需画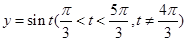 的图象和
的图象和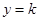 即可,从图象观察,可得实数
即可,从图象观察,可得实数 的取值范围.
的取值范围.(1)由
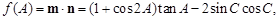
即
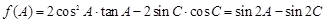 ,
,又因为
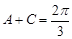 ,所以
,所以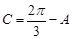 代入上式得,
代入上式得,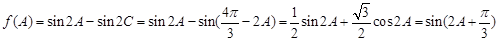
由
 ,得
,得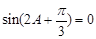 ,
,又
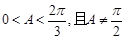 ,所以
,所以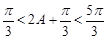 ,且
,且 5分
5分也所以
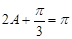 ,即
,即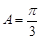 ,从而
,从而 为正三角形,
为正三角形,所以
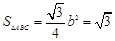 8分
8分(2)由(1)知
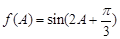 ,令
,令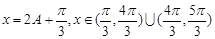 ,
,则方程
 有两个不同的实数解等价于
有两个不同的实数解等价于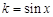 在
在 上有两上不同实根,作出
上有两上不同实根,作出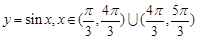 草图如右,
草图如右,可知当
 或
或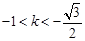 时,直线
时,直线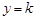 与曲线
与曲线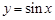 有两个交点,符合题意,故实数
有两个交点,符合题意,故实数 的取值范围为
的取值范围为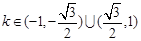 . 12分
. 12分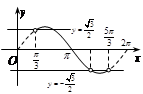

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
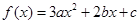 ,且有
,且有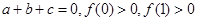 .
.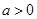 ,且
,且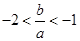 ;
;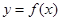 在区间
在区间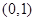 内有两个不同的零点.
内有两个不同的零点. ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与 ×S成正比,比例系数为
×S成正比,比例系数为 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S= 时。
时。
 ,使总淋雨量
,使总淋雨量 的两个极值点,且
的两个极值点,且 则b的最大值为_________.
则b的最大值为_________. 在
在 上的最大值为
上的最大值为 ,则函数
,则函数
 个
个 个
个 个
个 个
个 ,则﹣1+2i的原象为( )
,则﹣1+2i的原象为( ) 若
若 ,则
,则
 ,若
,若 ,则
,则 的值为 .
的值为 .