题目内容
设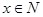 满足
满足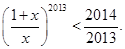 数列
数列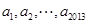 是公差为
是公差为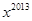 ,首项
,首项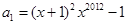 的等差数列; 数列
的等差数列; 数列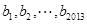 是公比为
是公比为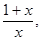 首项
首项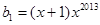 的等比数列,求证:
的等比数列,求证: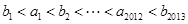 。
。
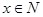 满足
满足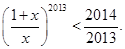 数列
数列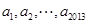 是公差为
是公差为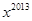 ,首项
,首项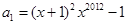 的等差数列; 数列
的等差数列; 数列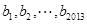 是公比为
是公比为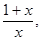 首项
首项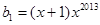 的等比数列,求证:
的等比数列,求证: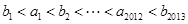 。
。用数学归纳法证明。
试题分析:首先,
 , 2分
, 2分 。 4分
。 4分 6分
6分用归纳法证明
 。
。由于
 ,即i=1成立。 8分
,即i=1成立。 8分假设
 成立,
成立,则


 。 14分
。 14分所以,
 。
。归纳证明
 ,
,首先
 ,假设
,假设 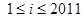 成立,
成立,则

 。 17分
。 17分故命题成立。
点评:难题,本题综合性较强,综合考查等差数列、等比数列的通项公式,数列不等式,数学归纳法等,在不等式的证明过程中,两次使用数学归纳法,一般来说较难想到。

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 个图形中有
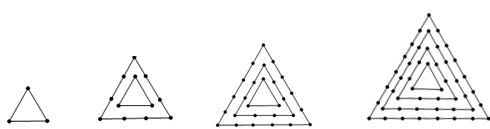
个图形中有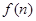 .
.
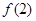 ,
, ,
,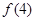 ,
, ;
;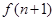 的关系,并求出
的关系,并求出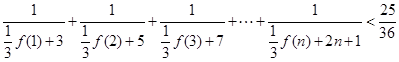 (
(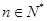 ).
).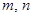 是正数,证明:
是正数,证明: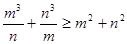 .
. 2c.
2c.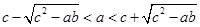 .
. 中,不等式
中,不等式 成立;在凸四边形ABCD中,
成立;在凸四边形ABCD中, 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式 成立,,依此类推,在凸n边形
成立,,依此类推,在凸n边形 中,不等式
中,不等式 __ ___成立.
__ ___成立.  证明:
证明: .
.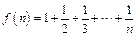 (
(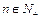 ),经计算得
),经计算得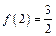 ,
,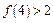 ,
,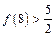 ,
,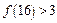 ,
,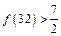 ,推测当
,推测当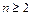 时,有不等式 成立.
时,有不等式 成立.