Question

如图，在直-棱柱ABO-A′B′O′中，OO′=4，OA=4，OB=3，∠AOB=90°，D是线段A′B′的中点，P是侧棱BB′上的一点，若OP⊥BD，求OP与底面AOB所成角的大小（结果用反三角函数值表示）

Answer 1

分析：如图，以O点为原点建立空间直角坐标系．求出B，D．设P（3，0，z），推出

BD

={ -

3

2

 ， 2 ， 4 }，

OP

={ 3 ， 0 ， z }．利用

BD

•

OP

=-

9

2

+4z=0.z=

9

8

．说明∠POB是OP与底面AOB所成的角，然后求出，
∴∠POB=arctan

3

8

解答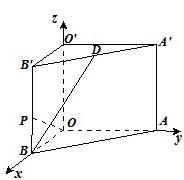：解：如图，以O点为原点建立空间直角坐标系．
由题意，有B（3，0，0），D ( 

3

2

 ， 2 ， 4 )．
设P（3，0，z），则

BD

={ -

3

2

 ， 2 ， 4 }，

OP

={ 3 ， 0 ， z }．
∵BD⊥OP，∴

BD

•

OP

=-

9

2

+4z=0.z=

9

8

．
∵BB′⊥平面AOB，
∴∠POB是OP与底面AOB所成的角.tan∠POB=

3

8

，
∴∠POB=arctan

3

8

．

点评：本题是基础题，利用空间直角坐标系通过向量的计算，考查直线与平面所成角的求法，空间想象能力，计算能力，常考题型．