题目内容
 (2013•泉州模拟)已知ω>0,函数f(x)=sinωx•cosωx+
(2013•泉州模拟)已知ω>0,函数f(x)=sinωx•cosωx+| 3 |
| ||
| 2 |
(Ⅰ)试求w的值;
(Ⅱ)在图中作出函数f(x)在区间[0,π]上的图象,并根据图象写出其在区间[0,π]上的单调递减区间.
分析:(Ⅰ)利用倍角公式和两角差的正弦公式即可化简函数f(x)=sinωx•cosωx+
sin2ωx-
=
sin2ωx-
cos2ωx=sin(2ωx-
),再利用周期公式即可得出ω.
(II)利用f(x)=sin(2x-
),x∈[0,π],找出区间端点、最大值点、最小值点及函数的零点并列对应值表,描点,并参照弦形曲线的走向特征,用光滑曲线把各对应点顺次联结起来画图,得函数f(x)在区间[0,π]上的图象及其单调递减区间.
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
(II)利用f(x)=sin(2x-
| π |
| 3 |
解答:解:(Ⅰ)函数f(x)=sinωx•cosωx+
sin2ωx-
=
sin2ωx-
cos2ωx=sin(2ωx-
).
因为函数f(x)的最小正周期为T=
=π,且ω>0,
所以ω=1.
(Ⅱ)因为f(x)=sin(2x-
),x∈[0,π].
列对应值表:
描点,并参照弦形曲线的走向特征,用光滑曲线把各对应点顺次联结起来画图,得函数f(x)在区间[0,π]上的图象如图所示.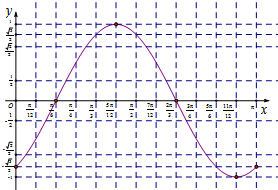
根据图象可得单调递减区间为[
,
].
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
因为函数f(x)的最小正周期为T=
| 2π |
| |ω| |
所以ω=1.
(Ⅱ)因为f(x)=sin(2x-
| π |
| 3 |
列对应值表:
| x | 0 |
|
|
|
|
π | ||||||||||
2x-
|
-
|
0 |
|
π |
|
| ||||||||||
| f(x) | -
|
0 | 1 | 0 | -1 | -
|

根据图象可得单调递减区间为[
| 5π |
| 12 |
| 11π |
| 12 |
点评:本小题主要考查三角恒等变型、三角函数的图象和性质等基础知识,考查运算求解能力,考查函数与方程思想等.

练习册系列答案
相关题目
 (2013•泉州模拟)如图,等腰梯形ABCD中,AB∥CD且AB=2,AD=1,DC=2x(x∈(0,1)).以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为 ( )
(2013•泉州模拟)如图,等腰梯形ABCD中,AB∥CD且AB=2,AD=1,DC=2x(x∈(0,1)).以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为 ( ) (2013•泉州模拟)设全集U=R,A={x|x(x+3)<0},B={x|x<-1},则图中阴影部分表示的集合为( )
(2013•泉州模拟)设全集U=R,A={x|x(x+3)<0},B={x|x<-1},则图中阴影部分表示的集合为( )