题目内容
5.已知f(x)=$\frac{1}{2}$log${\;}_{\frac{1}{2}}$($\frac{1}{2}$x)•log${\;}_{\frac{1}{2}}$($\frac{1}{4}$x),x∈[2,8],求值域.分析 根据对数的运算法则,利用换元法,转化为一元二次函数形式,利用一元二次函数的性质进行求解即可.
解答 解:f(x)=$\frac{1}{2}$log${\;}_{\frac{1}{2}}$($\frac{1}{2}$x)•log${\;}_{\frac{1}{2}}$($\frac{1}{4}$x)=$\frac{1}{2}$(log${\;}_{\frac{1}{2}}$$\frac{1}{2}$+log${\;}_{\frac{1}{2}}$x)•(log${\;}_{\frac{1}{2}}$$\frac{1}{4}$+log${\;}_{\frac{1}{2}}$x)
=$\frac{1}{2}$(1+log${\;}_{\frac{1}{2}}$x)•(2+log${\;}_{\frac{1}{2}}$x),
令t=log${\;}_{\frac{1}{2}}$x,x∈[2,8],
则t∈[-3,-1],
则函数等价为y=$\frac{1}{2}$(1+t)•(2+t)=$\frac{1}{2}$(t2+3t+2)=$\frac{1}{2}$(t+$\frac{3}{2}$)2+$\frac{1}{8}$,
∵t∈[-3,-1],
∴当t=-$\frac{3}{2}$时,y最小为$\frac{1}{8}$,
当t=-3时,y取得最大值y=1,
故函数的值域为[$\frac{1}{8}$,1].
点评 本题主要考查对数函数的值域的求解,利用换元法结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.在△ABC中,|$\overrightarrow{BC}$|•$\overrightarrow{GA}$+|$\overrightarrow{AC}$|•$\overrightarrow{GB}$+|$\overrightarrow{AB}$|•$\overrightarrow{GC}$=$\overrightarrow{0}$,其中G是三角形的重心,则△ABC的形状是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
15.如图所示的是一个几何体的三视图,则它的表面积为( )
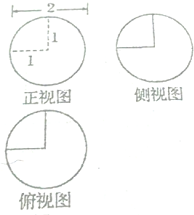

| A. | 4π | B. | $\frac{15π}{4}$ | C. | 5π | D. | $\frac{17π}{4}$ |