题目内容
(1)等比数列 中,对任意
中,对任意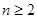 ,
, 时都有
时都有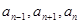 成等差,求公比
成等差,求公比 的值
的值
(2)设 是等比数列
是等比数列 的前
的前 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由
(3)设等比数列 的公比为
的公比为 ,前
,前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出 与
与 满足的关系;若不存在,请说明理由
满足的关系;若不存在,请说明理由
【答案】
解:(1)当 ,
,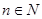 时有
时有


解得 或
或 ……………………………………5分
……………………………………5分
(2)当 时
时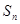
 ,显然
,显然 不是等差数列,
不是等差数列,
所以 ,
,
由 成等差得
成等差得
 或
或 (不合题意)所以
(不合题意)所以 ;
;
所以
即一定有 成等差数列。…………………………………11分
成等差数列。…………………………………11分
(3)假设存在正整数 ,使
,使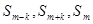 成等差且
成等差且 也成等差。
也成等差。
当 时
时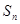
 ,显然
,显然 不是等差数列,
不是等差数列,
所以 ,
, ……………………………13分
……………………………13分
由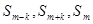 成等差得
成等差得

 或
或 …………16分
…………16分
当 为偶数时,
为偶数时, ,则有
,则有 且
且 ;
;
当 为奇数时,
为奇数时, ;
; ,
,
综上所述,存在正整数 (
( )满足题设,
)满足题设,
当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时, 。………………………18分
。………………………18分
【解析】略

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目