题目内容
下列命题中所有正确的命题是:______.
(1)不同的两个数a,b的等差中项A的绝对值必大于它们的等比中项G的绝对值.(等差中项A,等比中项G均存在)
(2)无穷等差数列中有三项是13,25,41,则2013一定是此数列中的一项.
(3)等比数列{an}中所有项均为正数,并且公比q≠1,则a2+a6>a3+a5.
(4)对任何数列{an}(n≥3),都存在一个等差数列{xn}与一个等比数列{yn},使得对任何n∈N*,an=xn+yn.
(1)不同的两个数a,b的等差中项A的绝对值必大于它们的等比中项G的绝对值.(等差中项A,等比中项G均存在)
(2)无穷等差数列中有三项是13,25,41,则2013一定是此数列中的一项.
(3)等比数列{an}中所有项均为正数,并且公比q≠1,则a2+a6>a3+a5.
(4)对任何数列{an}(n≥3),都存在一个等差数列{xn}与一个等比数列{yn},使得对任何n∈N*,an=xn+yn.
若两个数a,b存在等比中项G,则这两个数同号,由基本不等式易得(1)成立,
若无穷等差数列是首项41的递减数列,则满足无穷等差数列中有三项是13,25,41,但2013必不为数列中的某项,故(2)错误;
等比数列{an}中所有项均为正数,则q>0,则a2+a6=a2(1+q4),a3+a5=a2(q+q3),
∵(1+q4)-(q+q3)=(1-q)2(q2+q+1)>0恒成立,故a2+a6>a3+a5,即(3)正确
若无穷等差数列是首项41的递减数列,则满足无穷等差数列中有三项是13,25,41,但2013必不为数列中的某项,故(2)错误;
等比数列{an}中所有项均为正数,则q>0,则a2+a6=a2(1+q4),a3+a5=a2(q+q3),
∵(1+q4)-(q+q3)=(1-q)2(q2+q+1)>0恒成立,故a2+a6>a3+a5,即(3)正确

练习册系列答案
相关题目
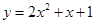 在
在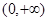 上是增函数;②函数
上是增函数;②函数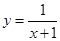 在
在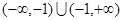 上是减函数;③函数
上是减函数;③函数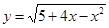 的单调区间是[-2,+∞);④已知
的单调区间是[-2,+∞);④已知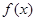 在R上是增函数,若
在R上是增函数,若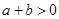 ,则有
,则有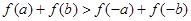 .其中正确命题的序号是______________.
.其中正确命题的序号是______________.