题目内容
（本题满分12分，第1小题6分，第小题6分）
设函数
的定义域为集合A，函数
的定义域为集合B。
（1）求A∩B；
（2）若
，求实数
的取值范围。
（1）A
B=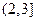
（2）
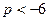
解析
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
寒假创新型自主学习第三学期寒假衔接系列答案题目内容
（本题满分12分，第1小题6分，第小题6分）
设函数的定义域为集合A，函数的定义域为集合B。
（1）求A∩B；
（2）若，求实数的取值范围。
（1）AB=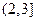
（2）
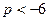
解析
寒假创新型自主学习第三学期寒假衔接系列答案
满足下列条件：
时，其最小值为0，且
成立；
时，
恒成立．
的值；
的解析式；
,使得存在
，只要当
时，就有
成立
是奇函数．
的单调性（不必说明单调性理由）；
，不等式
恒成立，求
的取值范围．
是R上的偶函数,且当
时,函数的解析式为
的值; 
上是减函数;
时,函数的解析式;
，判断函数
在
上的单调性并用定义证明
在
上是减函数。
，
是常数．
在点
的切线经过
轴上一个定点；
对
恒成立，求
）
的单调区间．
，x ∈[ 3 , 5 ] ,
为何值时，方程
有一个解？有两个解？有三个解？