题目内容
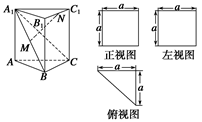
如图所示,已知空间四边形ABCD的各边和对角线的长都等于a,点M、N分别是AB、CD的中点.
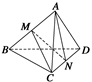
(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.

(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.
(1)证明略(2)MN的长为 a. (3)异面直线AN与CM所成角的余弦值为
a. (3)异面直线AN与CM所成角的余弦值为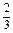
 a. (3)异面直线AN与CM所成角的余弦值为
a. (3)异面直线AN与CM所成角的余弦值为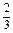
(1)设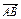 =p,
=p, 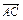 =q,
=q, =r.
=r.
由题意可知:|p|=|q|=|r|=a,且p、q、r三向量两两夹角均为60°.
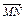 =
= -
-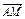 =
= (
(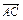 +
+ )-
)-
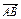
= (q+r-p), 2分
(q+r-p), 2分
∴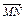 ·
·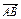 =
= (q+r-p)·p
(q+r-p)·p
= (q·p+r·p-p2)
(q·p+r·p-p2)
= (a2·cos60°+a2·cos60°-a2)=0.
(a2·cos60°+a2·cos60°-a2)=0.
∴MN⊥AB,同理可证MN⊥CD. 4分
(2)由(1)可知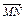 =
= (q+r-p)
(q+r-p)
∴|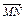 |2=
|2=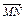 2=
2=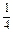 (q+r-p)2 6分
(q+r-p)2 6分
=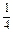 [q2+r2+p2+2(q·r-p·q-r·p)]
[q2+r2+p2+2(q·r-p·q-r·p)]
=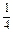 [a2+a2+a2+2(
[a2+a2+a2+2(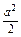 -
-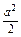 -
-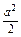 )
)
=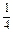 ×2a2=
×2a2=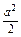 .
.
∴|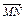 |=
|=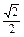 a,∴MN的长为
a,∴MN的长为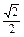 a. 10分
a. 10分
(3) 设向量 与
与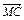 的夹角为
的夹角为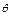 .
.
∵ =
= (
(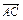 +
+ )=
)= (q+r),
(q+r),
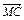 =
=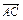 -
-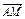 =q-
=q- p,
p,
∴ ·
·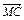 =
= (q+r)·(q-
(q+r)·(q- p)
p)
= (q2-
(q2- q·p+r·q-
q·p+r·q- r·p)
r·p)
= (a2-
(a2- a2·cos60°+a2·cos60°-
a2·cos60°+a2·cos60°- a2·cos60°)
a2·cos60°)
= (a2-
(a2-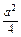 +
+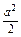 -
-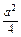 )=
)=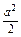 . 12分
. 12分
又∵| |=|
|=|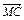 |=
|= ,
,
∴ ·
·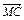 =|
=| |·|
|·|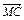 |·cos
|·cos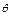
= ·
· ·cos
·cos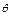 =
=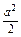 .
.
∴cos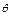 =
=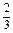 , 14分
, 14分
∴向量 与
与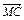 的夹角的余弦值为
的夹角的余弦值为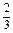 ,从而异面直线AN与CM所成角的余弦值为
,从而异面直线AN与CM所成角的余弦值为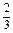 .
.
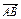 =p,
=p, 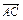 =q,
=q, =r.
=r.由题意可知:|p|=|q|=|r|=a,且p、q、r三向量两两夹角均为60°.
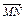 =
= -
-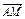 =
= (
(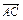 +
+ )-
)-
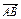
=
 (q+r-p), 2分
(q+r-p), 2分∴
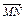 ·
·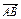 =
= (q+r-p)·p
(q+r-p)·p=
 (q·p+r·p-p2)
(q·p+r·p-p2)=
 (a2·cos60°+a2·cos60°-a2)=0.
(a2·cos60°+a2·cos60°-a2)=0.∴MN⊥AB,同理可证MN⊥CD. 4分
(2)由(1)可知
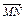 =
= (q+r-p)
(q+r-p)∴|
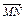 |2=
|2=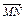 2=
2=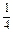 (q+r-p)2 6分
(q+r-p)2 6分=
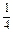 [q2+r2+p2+2(q·r-p·q-r·p)]
[q2+r2+p2+2(q·r-p·q-r·p)]=
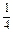 [a2+a2+a2+2(
[a2+a2+a2+2(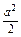 -
-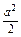 -
-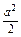 )
)=
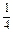 ×2a2=
×2a2=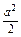 .
.∴|
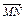 |=
|=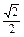 a,∴MN的长为
a,∴MN的长为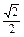 a. 10分
a. 10分(3) 设向量
 与
与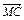 的夹角为
的夹角为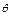 .
.∵
 =
= (
(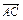 +
+ )=
)= (q+r),
(q+r),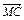 =
=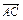 -
-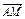 =q-
=q- p,
p,∴
 ·
·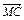 =
= (q+r)·(q-
(q+r)·(q- p)
p)=
 (q2-
(q2- q·p+r·q-
q·p+r·q- r·p)
r·p)=
 (a2-
(a2- a2·cos60°+a2·cos60°-
a2·cos60°+a2·cos60°- a2·cos60°)
a2·cos60°)=
 (a2-
(a2-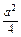 +
+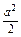 -
-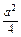 )=
)=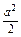 . 12分
. 12分又∵|
 |=|
|=|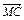 |=
|= ,
,∴
 ·
·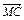 =|
=| |·|
|·|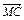 |·cos
|·cos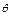
=
 ·
· ·cos
·cos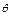 =
=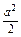 .
.∴cos
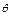 =
=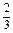 , 14分
, 14分∴向量
 与
与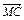 的夹角的余弦值为
的夹角的余弦值为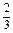 ,从而异面直线AN与CM所成角的余弦值为
,从而异面直线AN与CM所成角的余弦值为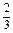 .
. 
练习册系列答案
相关题目
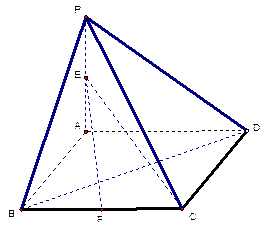
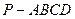 中,四边形
中,四边形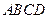 是正方形,
是正方形,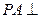 平面
平面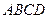 ,
,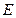 是
是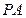 上的一点,
上的一点,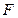 是
是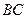 的中点
的中点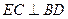 ;
;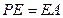 ,求证:
,求证: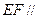 平面
平面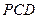 .
.
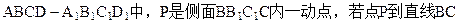 与直线
与直线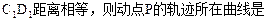
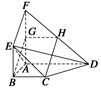
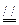
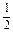 AD,BE
AD,BE ,
,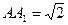 ,
, ,若
,若 为棱
为棱 中点.
中点. ∥平面
∥平面 ;
;
 与平面
与平面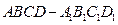 中,
中,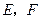 分别为
分别为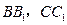 的中点.求
的中点.求 所成角的余弦值.
所成角的余弦值.