题目内容
正方体ABCD-A1B1C1D1中,对角线A1C与平面BDC1交于点O,AC、BD交于点M,求证:C1、O、M三点共线.
如图,∵AA1∥CC1,
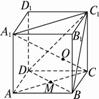
∴AA1、CC1确定一个平面A1C.
显然有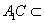 平面A1C,
平面A1C,
又∵A1C∩平面BC1D=O,AC∩BD=M,
∴点C1、O、M三点在平面A1C内,也在平面BC1D内,
从而C1、O、M三点都在这两个平面的交线上,即C1、O、M三点共线.

∴AA1、CC1确定一个平面A1C.
显然有
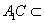 平面A1C,
平面A1C,又∵A1C∩平面BC1D=O,AC∩BD=M,
∴点C1、O、M三点在平面A1C内,也在平面BC1D内,
从而C1、O、M三点都在这两个平面的交线上,即C1、O、M三点共线.
空间直线和平面

练习册系列答案
相关题目
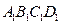 中,AB=2,
中,AB=2,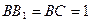 ,E为
,E为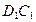 的中点,连结ED,EC,EB和DB,
的中点,连结ED,EC,EB和DB,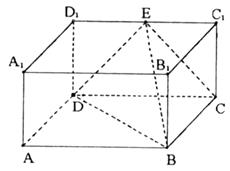
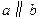 ,
,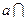 平面
平面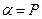 ,如图.求证:直线
,如图.求证:直线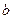 与平面
与平面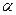 相交.
相交.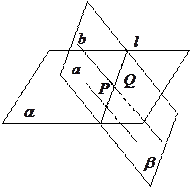
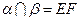 ,
,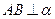 ,
,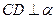 ,垂足分别为
,垂足分别为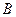 、
、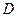 。若增加一个条件,就能推出
。若增加一个条件,就能推出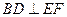 。现有:
。现有: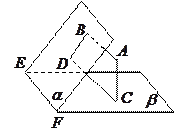
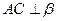 ;
;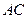 与
与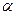 、
、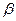 所成的角相等;
所成的角相等;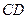 在
在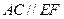 。
。