题目内容
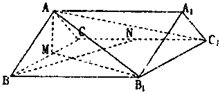如图，已知三棱柱ABC-A1B1C1中，AB=AC=5，BC=BB1=8，M，N分别为BC，CC1的中点．（1）求证：BN⊥AB1；
（2）求AC1与平面AMB1所成角的正弦值．
分析：（1）以M为原点建立空间坐标系分别求出BN与AB1的方向向量，判断两个向量数量积是否为0，即可得到BN⊥AB1；
（2）求出AC1的方向向量及平面AMB1的法向量，代入向量夹角公式，即可得到AC1与平面AMB1所成角的正弦值
（2）求出AC1的方向向量及平面AMB1的法向量，代入向量夹角公式，即可得到AC1与平面AMB1所成角的正弦值
解答：解：∵AB=AC，M为BC的中点．
∴AM⊥BC
∵三棱柱ABC-A1B1C1为直三棱柱
∴AM⊥平面B1C
取B1C1中点P，连接MP
以M为原点，MB，MP，MA方向为x，y，z轴正方向建立空间坐标系，
∵AB=AC=5，BC=BB1=8，M，N分别为BC，CC1的中点，
且AM=
=3
∴M（0，，0，0），A（0，0，3），B（4，0，0），C（-4，0，0），N（-4，4，0），C1（-4，8，0），B1（4，8，0）
（1）
=（-8，4，0），
=（4，8，-3），
∴
•
=0
即BN⊥AB1；
（2）由（1）知
=（-8，4，0）是平面AMB1的一个法向量
又∵
=（-4，8，-3）
设AC1与平面AMB1所成角为θ
则sinθ=
=
即AC1与平面AMB1所成角的正弦值为
∴AM⊥BC
∵三棱柱ABC-A1B1C1为直三棱柱
∴AM⊥平面B1C
取B1C1中点P，连接MP
以M为原点，MB，MP，MA方向为x，y，z轴正方向建立空间坐标系，
∵AB=AC=5，BC=BB1=8，M，N分别为BC，CC1的中点，
且AM=
| AB2-BM2 |
∴M（0，，0，0），A（0，0，3），B（4，0，0），C（-4，0，0），N（-4，4，0），C1（-4，8，0），B1（4，8，0）
（1）
| BN |
| AB1 |
∴
| BN |
| AB1 |
即BN⊥AB1；
（2）由（1）知
| BN |
又∵
| AC1 |
设AC1与平面AMB1所成角为θ
则sinθ=
|
| ||||
|
|
16
| ||
| 445 |
即AC1与平面AMB1所成角的正弦值为
16
| ||
| 445 |
点评：本题考查的知识点是用空间向量求直线与平面的夹角，其中建立空间坐标系，求出各点坐标，进而得到直线的方向向量和平面法向量的坐标是解答的关键．
练习册系列答案
相关题目
如图，已知三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AC=BC=2，AA1=4，
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M，N分别是CC1，BC的中点，点P在直线A1B1上，且
如图，已知三棱柱ABC-A1B1C1的所有棱长均为2，且A1A⊥底面ABC，D为AB的中点，G为△ABC1的重心，则|
如图，已知三棱柱ABC-A1B1C1中，AA1⊥平面ABC，AB=BC，∠ABC=90°，D为AC中点．