题目内容
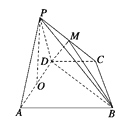
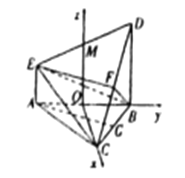
【题目】如图,在多面体![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]() 是边长为4的等边三角形,
是边长为4的等边三角形, ![]() ,
, ![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ,
, ![]() 是线段
是线段![]() 上一点.
上一点.

(Ⅰ)若![]() 是线段
是线段![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)利用面面垂直的判定定理即可证明;
(Ⅱ)建立空间直角坐标系,求出两个平面的法向量,利用两个法向量的夹角即可求解
试题解析:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() 是
是![]() 在平面
在平面![]() 上的射影,
上的射影, ![]() 即是
即是![]() 与平面
与平面![]() 所成角.
所成角.
∵![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ,
,
∴![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
∴![]() ,而
,而![]() ,
,
∴![]() ,∴
,∴![]() .
.
法一:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .
.
∵![]() 是等边三角形, ∴
是等边三角形, ∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 是线段
是线段![]() 的中点,
的中点,
∴![]() ,且
,且![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,且
,且![]() .
.
∴![]() ,且
,且![]() ,四边形
,四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
法二:取![]() 的中点为
的中点为![]() ,以
,以![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
而![]() 平面
平面![]() ,且
,且![]() .
.
所以![]() 平面
平面![]()
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
(Ⅱ)解:由(Ⅰ)知,当![]() 是线段
是线段![]() 的中点时,可得
的中点时,可得![]() 平面
平面![]() ,
,
又![]() ,
,
则可取平面![]() 的一个法向量
的一个法向量![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,则
,则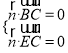 ,
,
又![]() ,
, ![]() ,
,
所以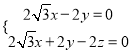 .
.
取![]() ,则
,则![]() ,
, ![]() ,即
,即![]() ,
,
则![]()
![]() ,
,
![]() ,
,
所以二面角![]() 的平面角的正弦值为
的平面角的正弦值为![]() .
.

【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?