题目内容
【题目】如图所示,在四棱锥P—ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4![]() .
.
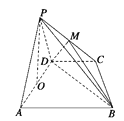
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2)求四棱锥P-ABCD的体积.
【答案】(1)证明见解析;(2) 16![]() .
.
【解析】试题分析:
(1)证得AD⊥BD,而面PAD⊥面ABCD,∴BD⊥面PAD,∴面MBD⊥面PAD.
(2)作辅助线PO⊥AD,则PO为四棱锥P—ABCD的高,求得S四边形ABCD=24.∴VP—ABCD=16![]() .
.
试题解析:
(1)证明:在△ABD中,∵AD=4,BD=8,AB=4![]() ,∴AD2+BD2=AB2.∴AD⊥BD.
,∴AD2+BD2=AB2.∴AD⊥BD.
又∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,BD面ABCD,∴BD⊥面PAD.
又BD面BDM,∴面MBD⊥面PAD.
(2)解:过P作PO⊥AD,
∵面PAD⊥面ABCD,∴PO⊥面ABCD,即PO为四棱锥P—ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=2![]() .
.
在底面四边形ABCD中,AB∥DC,AB=2DC,∴四边形ABCD为梯形.
在Rt△ADB中,斜边AB边上的高为![]() =
=![]() ,此即为梯形的高.
,此即为梯形的高.
∴S四边形ABCD=![]() ×
×![]() =24.
=24.
∴VP—ABCD=![]() ×24×2
×24×2![]() =16
=16![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目