题目内容
【题目】Fibonacci数列又称黄金分割数列,因为当n趋向于无穷大时,其相邻两项中的前项与后项的比值越来越接近黄金分割数![]() .已知Fibonacci数列的递推关系式为
.已知Fibonacci数列的递推关系式为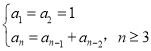 .
.
(1)证明:Fibonacci数列中任意相邻三项不可能成等比数列;
(2)Fibonacci数列{an}的偶数项依次构成一个新数列,记为{bn},证明:{bn+1-H2·bn}为等比数列.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用反证法,假设存在![]() ,
,![]() ,
,![]() 三项成等比数列,则
三项成等比数列,则![]() ,进而由已知关系证得
,进而由已知关系证得![]() 是无理数,这与其递推公式中反应的为有理数矛盾,得证;
是无理数,这与其递推公式中反应的为有理数矛盾,得证;
(2)由题表示![]() ,进而由已知
,进而由已知![]() 的递推关系表示出
的递推关系表示出![]() 的递推公式,再构造等比数列
的递推公式,再构造等比数列![]() ,进而由一一对应关系计算出对应参量,最后由等比数列定义得证.
,进而由一一对应关系计算出对应参量,最后由等比数列定义得证.
(1)证明:(反证法)假设存在![]() ,
,![]() ,
,![]() 三项成等比数列,则
三项成等比数列,则![]() ,
,
所以![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
由条件可知Fibonacci数列的所有项均大于0,所以![]() ,
,
又Fibonacci数列的所有项均为整数(由递推公式),所以![]() 应该为有理数,
应该为有理数,
这与![]() (无理数)矛盾(其相邻两项中的前项与后项的比值越来越接近黄金分割数,而不是恰好相等),
(无理数)矛盾(其相邻两项中的前项与后项的比值越来越接近黄金分割数,而不是恰好相等),
所以假设不成立,故原命题成立.
(2)证明:由条件得![]() ,
,![]() ,
,
所以![]() ,
,
即![]() ,
,
设![]() ,则
,则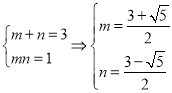 或
或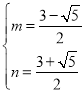
所以![]() 或
或![]()
所以![]() ,所以
,所以![]() 为等比数列,公比为
为等比数列,公比为![]() .
.

练习册系列答案
相关题目