题目内容
已知集合A={x|x2+a≤(a+1)x,a∈R}.(1)是否存在实数a,使得集合A中所有整数的元素和为28?若存在,求出符合条件的a,若不存在,请说明理由.
(2)若以a为首项,a为公比的等比数列前n项和记为Sn,对于任意的n∈N+,均有Sn∈A,求a的取值范围.
【答案】分析:(1)利用因式分解法求解含字母的一元二次不等式,写解集时要注意对字母a进行讨论,注意存在性问题的解决方法,只需找出合题意的实数a即可;
(2)写出该数列的通项公式是解决本题的关键.注意对字母a的讨论,利用Sn∈A得出关于a的不等式或者找反例否定某种情况,进行探求实数a的取值范围.
解答:解:(1)当a<1时,A={x|a≤x≤1},不符合;
当a≥1时,A={x|-2≤x≤1},设a∈[n,n+1),n∈N,则
1+2++n=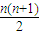 =28,
=28,
所以n=7,即a∈[7,8)
(2)当a≥1时,A={x|1≤x≤a}.而S2=a+a2∉A,故a≥1时,不存在满足条件的a;
当0<a<1时,A={a≤x≤1},而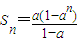 是关于n的增函数,
是关于n的增函数,
所以Sn随n的增大而增大,
当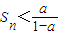 且无限接近
且无限接近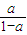 时,对任意的n∈N+,Sn∈A,只须a满足
时,对任意的n∈N+,Sn∈A,只须a满足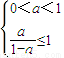 解得
解得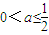 .
.
当a<-1时,A={x|a≤x≤1}.
而S3-a=a2+a3=a2(1+a)<0,S3∉A故不存在实数a满足条件.
当a=-1时,A={x|-1≤x≤1}.S2n-1=-1,S2n=0,适合.
⑤当-1<a<0时,A={x|a≤x≤1}.S2n+1=S2n-1+a2n+a2n+1=S2n-1+a2n+a2n+1=S2n-1+a2n(1+a)>S2n-1,S2n+2=S2n+a2n+1+a2n+2=S2n+a2n+1+a2n+2=S2n+a2n+1(1+a)<S2n,
∴S2n-1<S2n+1,S2n+2<S2n,且S2=S1+a2>S1.
故S1<S3<S5<…<S2n+1<S2n<S2n-2<…<S4<S2.
故只需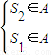 即
即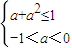
解得-1<a<0.
综上所述,a的取值范围是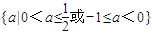 .
.
点评:本题属于含字母二次不等式解法的综合问题,关键要对字母进行合理的讨论.注意存在性问题问题的解决方法,注意分类讨论思想的运用,注意等比数列中有关公式的运用.
(2)写出该数列的通项公式是解决本题的关键.注意对字母a的讨论,利用Sn∈A得出关于a的不等式或者找反例否定某种情况,进行探求实数a的取值范围.
解答:解:(1)当a<1时,A={x|a≤x≤1},不符合;
当a≥1时,A={x|-2≤x≤1},设a∈[n,n+1),n∈N,则
1+2++n=
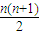 =28,
=28,所以n=7,即a∈[7,8)
(2)当a≥1时,A={x|1≤x≤a}.而S2=a+a2∉A,故a≥1时,不存在满足条件的a;
当0<a<1时,A={a≤x≤1},而
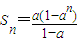 是关于n的增函数,
是关于n的增函数,所以Sn随n的增大而增大,
当
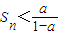 且无限接近
且无限接近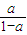 时,对任意的n∈N+,Sn∈A,只须a满足
时,对任意的n∈N+,Sn∈A,只须a满足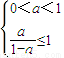 解得
解得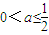 .
.当a<-1时,A={x|a≤x≤1}.
而S3-a=a2+a3=a2(1+a)<0,S3∉A故不存在实数a满足条件.
当a=-1时,A={x|-1≤x≤1}.S2n-1=-1,S2n=0,适合.
⑤当-1<a<0时,A={x|a≤x≤1}.S2n+1=S2n-1+a2n+a2n+1=S2n-1+a2n+a2n+1=S2n-1+a2n(1+a)>S2n-1,S2n+2=S2n+a2n+1+a2n+2=S2n+a2n+1+a2n+2=S2n+a2n+1(1+a)<S2n,
∴S2n-1<S2n+1,S2n+2<S2n,且S2=S1+a2>S1.
故S1<S3<S5<…<S2n+1<S2n<S2n-2<…<S4<S2.
故只需
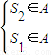 即
即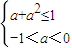
解得-1<a<0.
综上所述,a的取值范围是
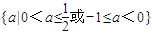 .
.点评:本题属于含字母二次不等式解法的综合问题,关键要对字母进行合理的讨论.注意存在性问题问题的解决方法,注意分类讨论思想的运用,注意等比数列中有关公式的运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目