题目内容
若对满足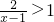
的任意实数x，使得不等式2x3+3x2≥6（6x+a）恒成立，求实数a的取值范围．
解：由已知得1＜x＜3，
设f（x）=2x3+3x2-36x-6a，x∈（1，3）…（4分）
∴f’（x）=6x2+6x-36，
由f’（x）=0得x=2，x=-3舍．
当1＜x＜2时，f′（x）＜0，
当2＜x＜3时，f′（x）＞0…（8分）
∴f（x）在x=2处取得最小值 f（2）=-44-6a≥0，
∴
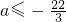．…（10分）
分析：由已知得1＜x＜3，设f（x）=2x3+3x2-36x-6a，x∈（1，3），故f‘（x）=6x2+6x-36，由f‘（x）=0得x=2，x=-3舍．由此能求出实数a的取值范围．
点评：本题考查利用导数求闭区间上函数最值的应用，解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．
设f（x）=2x3+3x2-36x-6a，x∈（1，3）…（4分）
∴f’（x）=6x2+6x-36，
由f’（x）=0得x=2，x=-3舍．
当1＜x＜2时，f′（x）＜0，
当2＜x＜3时，f′（x）＞0…（8分）
∴f（x）在x=2处取得最小值 f（2）=-44-6a≥0，
∴
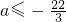．…（10分）分析：由已知得1＜x＜3，设f（x）=2x3+3x2-36x-6a，x∈（1，3），故f‘（x）=6x2+6x-36，由f‘（x）=0得x=2，x=-3舍．由此能求出实数a的取值范围．
点评：本题考查利用导数求闭区间上函数最值的应用，解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．
练习册系列答案
相关题目
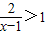的任意实数x，使得不等式2x3+3x2≥6（6x+a）恒成立，求实数a的取值范围．
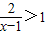的任意实数x，使得不等式2x3+3x2≥6（6x+a）恒成立，求实数a的取值范围．